Information Analysis (5.0.2)
Overview
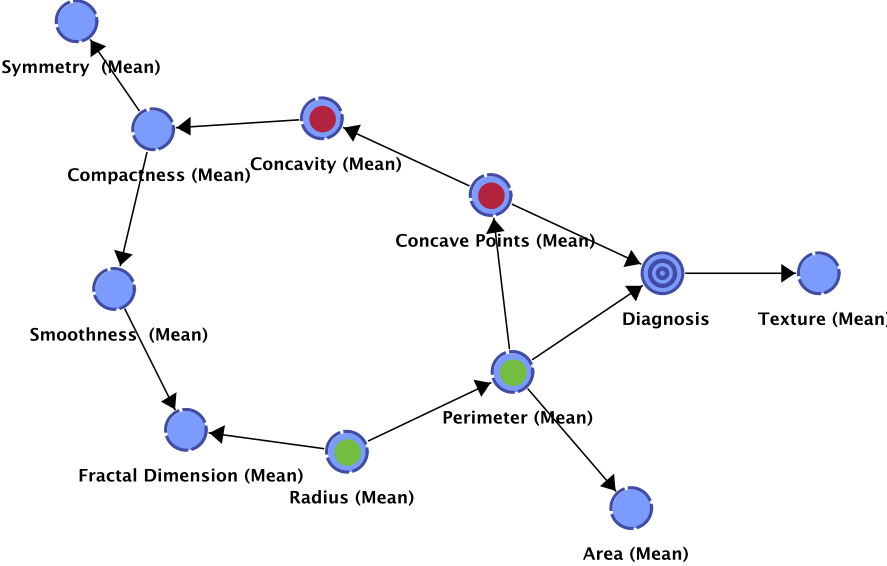
Information analysis with three sets of nodes (X, Y, and Z)
Clicking on the Select Nodes buttons allows defining three sets of nodes for analysis. The selection is done by directly selecting the nodes in the graph. By default, the Target node is associated with the Y set.
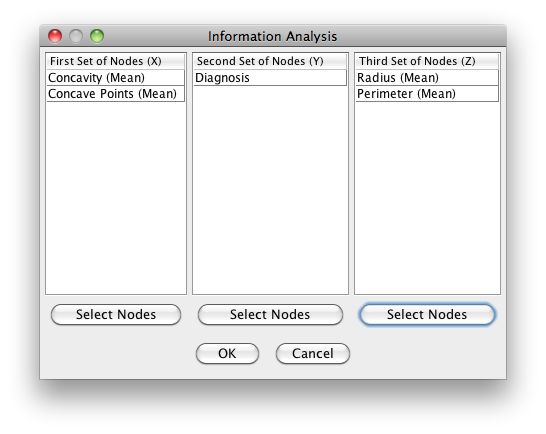
Information Analysis Report
Given the exponential growth of the state space, this analysis is only performed on the database.

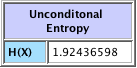
Unconditional Entropy
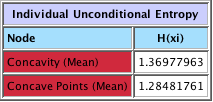
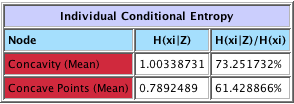
Conditional Entropy

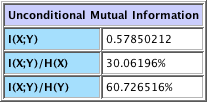
Unconditional Mutual Information
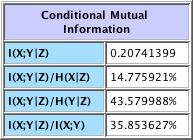
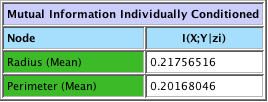
Conditional Mutual Information
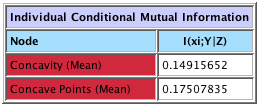
Total Correlation

Conditional Total Correlation

