Total Effects on Target Report

Context

• This analysis characterizes the relationships of selected nodes in a network with the Target Node by calculating unit effects and related statistics.
• Performing this analysis is often used as a reference point in a key driver analysis see Chapter 8.

Example

• The following example is taken from Chapter 8: Chapter 8: Probabilistic Structural Equation Models for Key Driver Analysis
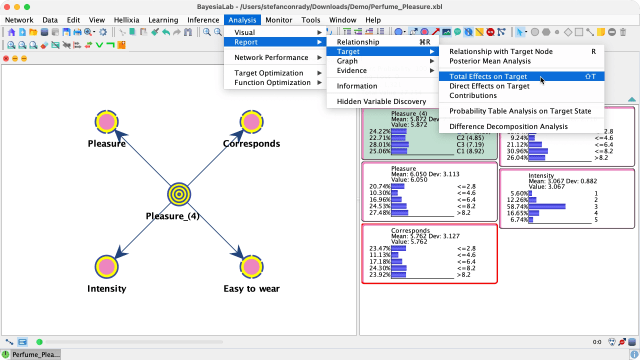
• The network below features a the Target Node at the center of the network for which we want to analyze its response to changes of the nodes connected to it.
  • The the node $Pleasure\_(4)$ is the Target Node.
  • The nodes $Pleasure$, $Corresponds$, $Easy\, to\, wear$, and $Intensity$ are the Driver Nodes under investigation.
  • In traditional statistics, the Target Node would be the dependent variable, and the Driver Nodes would be considered independent variables.
    

Usage

• Make sure you have defined a Target Node.

• In Validation Mode F5, select the nodes of interest and go to Menu > Analysis > Report > Target > Total Effects on Target > Total Effects.

• If you have not selected any node, BayesiaLab will use all connected and observable nodes for the analysis.

  

• This analysis creates a report, which is displayed in a new window.

Report

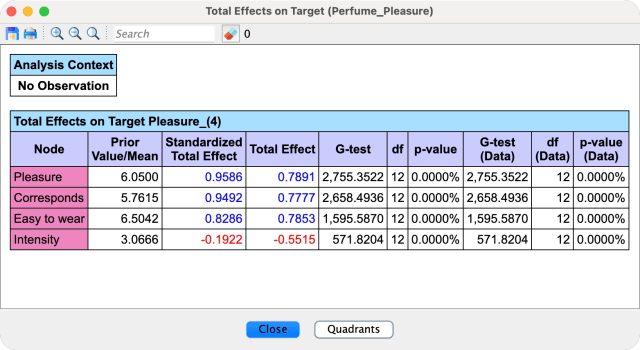
Interpretation

• To interpret this report, we first need to provide formal definitions of the metrics that are presented.
• Furthermore, we must reference the Target Mean Analysis function, which calculates the Total Effects Curves that serve as the basis of this report.

Total Effect Definition

• The Total Effect of a Driver Node on a Target Node is the derivative of the Total Effects Curve, computed at the a priori mean of that node, i.e., Delta Mean=0.

  $TE = {{{\delta_y}} \over {{\delta_x}}}$

  where $X$ is the Driver Node and $Y$ is the Target Node.

• In words, $\delta_x$ represents a small change in the mean value of a Driver Node.

• $\delta_y$ is the inferred change in the mean value of the Target Node.

• The Total Effect is the ratio of these two values.

• We borrow a plot of the Total Effects Curves produced by the Target Mean Analysis to illustrate the derivative calculation.

  

• In this plot, Delta Mean=0 is marked with a black dashed vertical line, indicating the mean value of all Driver Nodes.

• For the Driver Node $Intensity$, its derivative — at its mean value — is illustrated with a cyan-colored dashed tangent.

• So, Total Effect of $Intensity$ is the derivative of the curve, which is the same as the slope of the plotted tangent.

Limitations

• The Driver Node we selected for this example, $Intensity$, immediately highlights the limitations of the Total Effects on Target Report.
• While it is possible to calculate the Total Effect of $Intensity$, its corresponding curve shows that the estimated value of the Total Effect is not at all a fair representation of the entire dynamic between this $Intensity$ and the Target Node.
• However, we can see that the other Driver Nodes seem to have a fairly linear relationship with the Target Node. The slopes of their curves remain unchanged across their respective x-ranges. For them, reporting the Total Effect characterizes their dynamics very well.

Standardized Total Effect

• In addition to the Total Effect, the Standardized Total Effect is also shown in the report.

• It represents the Total Effect multiplied by the ratio of the standard deviation of the Driver Node and the standard deviation of the Target Node.

• The Standardized Total Effect normalizes the Total Effect by taking into account the ratio between the standard deviations of the Driver Nodes (x) and the Target Node (y).

  $STE = {{{\delta _y}} \over {{\delta _x}}} \times {{{\sigma _x}} \over {{\sigma _y}}}$

• In the Total Effects Report, and for both the Total Effects and Standardized Total Effect, positive and negative values are displayed in blue and red, respectively.

Independence Tests

• In addition to the effects, the report includes independence test metrics:
  • ${\chi}^2$ or G-test.
    • You can select which test to use, i.e., ${\chi}^2$ or G-test, under Menu > Window > Preferences > Tools > Statistical Tools.
  • Degree of Freedom: Indicates the degree of freedom between each Driver Node and the Target Node.
  • p-value: Reports the p-value calculated with selected independence test.
  • If a dataset is associated with the network, the independence tests are also performed on the basis of the dataset.

Quadrant Chart

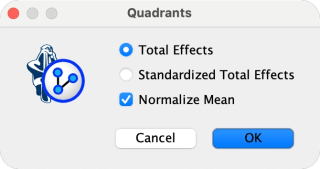
• Clicking the button Quadrants at the bottom of the report window produces a so-called Quadrant chart:

  • The Driver Nodes' marginal mean values are shown x-axis.

  • The y-axis shows the Total Effects or Standardized Total Effects, which were shown in the report.

  • You have a choice of displaying either metric in the pop-up window.

    

• Upon confirming your selection, a new window presents the Quadrant Chart.

• Each point in the Quadrant Chart represents a Driver Node.
• If a color is assigned to the nodes, the point will be shown in that color.
• The name of each Driver Node is displayed to the right of each point.
• When hovering over any of the displayed points with your cursor, the point's coordinates are shown in the top panel.
• The top panel also shows the number of points displayed as well as any evidence context.

Quadrant Chart Axes

• The chart is divided into four quadrants.
• The divider line on the x-axis is positioned at the mean value of all of the mean values, i.e., the mean of the mean.
• The divider line on the y-axis is positioned at the mean value of the all the nodes' calculated y metric, e.g., the mean of all Standardized Total Effects of the nodes on the Target Node, which is shown in this example.

Quadrant Interpretation

• Depending on the domain, there are various ways to interpret the quadrants.
• For instance, in the context of key driver analysis of overall customer satisfaction, the x-values of the Driver Nodes could represent the current satisfaction level of individual product attributes.
• The y-values show the importance of each Driver Node with the Target Node, such as overall satifaction with a product.
• In this context, one can read the quadrants as follows:
  • Quadrant 1 (top right): points in this quadrant represent drivers that have above average satisfaction and above average importance. Casually speaking, one could say, keep up the good work on these drivers.
  • Quadrant 2 (bottom right): the points in this quadrant have above-average satisfaction but are below average in terms of importance. One could say that his is the "overkill" zone.
  • Quadrant 3 (bottom left) features below-average drivers with below average importance. Generally speaking,
  • Quadrant 4 (top left) delineates the "area of opportunity." Drivers are below average in performance, have room to improve, and are important.

Quadrant Chart Options

• The Quadrant Chart offers you several options via its Context Menu:
  • Display the Driver Nodes' Long Names instead of their standard names.
  • Copy the chart content in multiple formats:
    • Bitmap, e.g., png or jpg.
    • Vector graphic, e.g., SVG or PDF.
    • Table of x-y coordinates of points on chart:
      • Formatted table in HTML format, which is practical for presentation purposes.
      • Plain table in text format for further editing.
  • Print the chart.
• The chart is automatically resized with the size of the window.