Step 1: Unsupervised Learning
As a first step, we need to exclude the node Purchase Intent, which will later serve as our Target Node. We do not want this node to become part of the structure that we will subsequently use for discovering hidden concepts. Likewise, we need to exclude the node Product, as it does not contain consumer feedback to be evaluated.
We can exclude nodes by selecting the Node Exclusion Mode and then clicking on the to-be-excluded node.
The upcoming series of steps is crucial. We now need to prepare a robust network on which we can later perform the clustering process. Given the importance, we recommend going through the full range of Unsupervised Learning algorithms and comparing the performance of each resulting network structure to select the best structure.
The objective is to increase our chances of finding the optimal network for our purposes. Given that the number of possible networks grows super-exponentially with the number of nodes, this is a significant challenge.
| Number of Nodes | Number of Possible Networks |
|---|---|
| 1 | 1 |
| 2 | 3 |
| 3 | 25 |
| 4 | 543 |
| 5 | 29,281 |
| 6 | 3.7815×10^6 |
| 7 | 1.13878×10^9 |
| 8 | 7.83702×10^11 |
| 9 | 1.21344×10^15 |
| 10 | 4.1751×10^18 |
| … | … |
| 47 | 8.98454×10^376 |
It may not be immediately apparent how such an astronomical number of networks could be possible. The illustration below shows how 3 nodes can be combined in 25 ways to form a network.

Needless to say, generating all 9×10^376 networks—based on 47 nodes—and then selecting the best one is completely intractable (for reference, it is estimated that there are between 1078 to 1082 atoms in the known, observable universe). So, an exhaustive search would only be feasible for a small subset of nodes.
As a result, we have to use heuristic search algorithms to explore a small part of this huge space in order to find a local optimum. However, a heuristic search algorithm does not guarantee to find the global optimum. This is why BayesiaLab offers a range of distinct learning algorithms, which all use different search spaces and search strategies:
- Bayesian networks for Maximum Weight Spanning Tree and Taboo.
- Essential Graphs for EQ and SopLEQ, i.e., graphs with edges and arcs representing classes of equivalent networks.
- Order of nodes for Taboo Order.
This diversity increases the probability of finding a solution close to the global optimum. Given adequate time and resources for learning, we recommend employing the algorithms in the following sequence to find the best solution:
- Maximum Weight Spanning Tree + Taboo
- Taboo (“from scratch”)
- EQ (“from scratch”) + Taboo
- SopLEQ + Taboo
- Taboo Order + Taboo
However, to keep the presentation compact, we only illustrate the learning steps for the EQ algorithm: Menu > Learning > Unsupervised Structural Learning > EQ.
The network generated by the EQ algorithm is shown below.
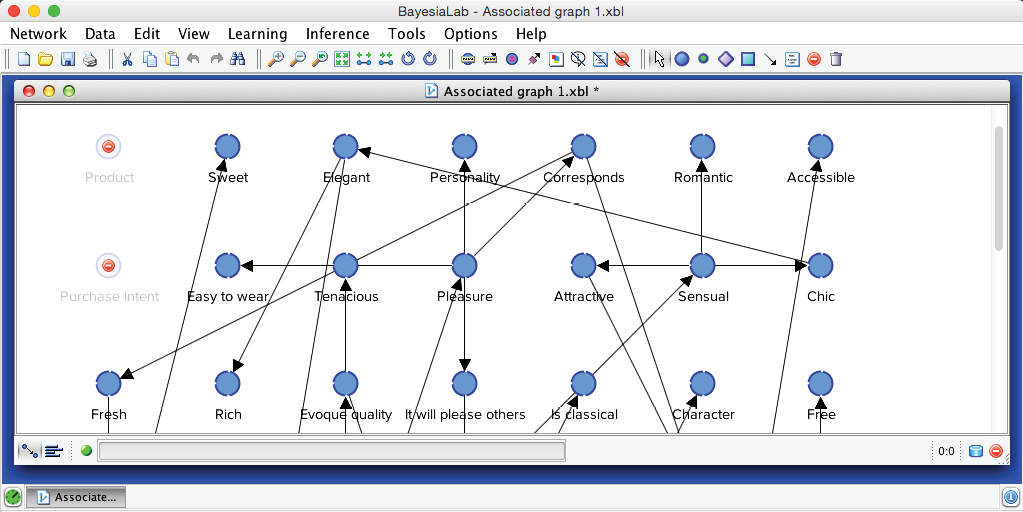
Pressing P and then clicking the Best-Fit icon , provides an interpretable view of the network. Additionally, rotating the network graph with the Rotate Left and Rotate Right buttons can help set a suitable view.
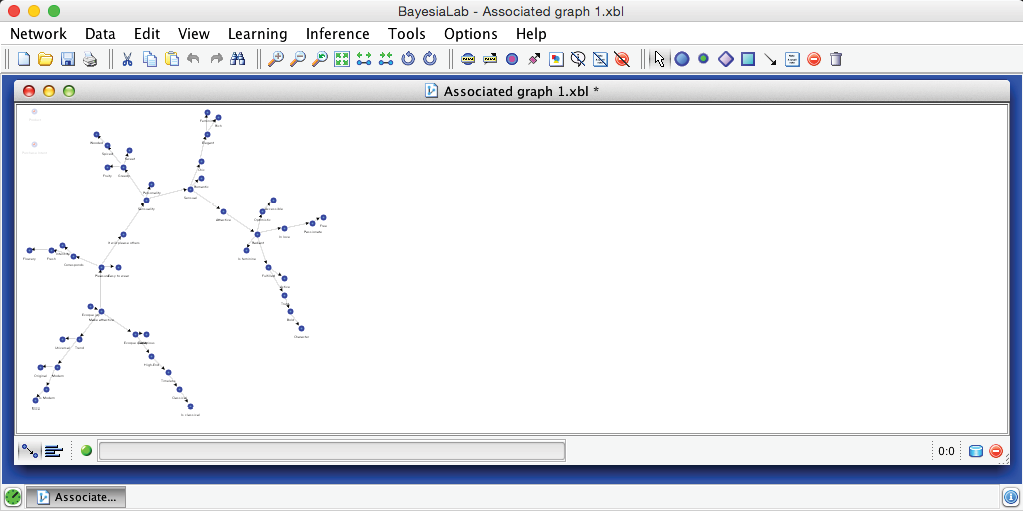
We now need to assess the quality of this network. Each of BayesiaLab’s Unsupervised Learning algorithms uses the Minimum Description Length (MDL) Score —internally—as the measure to optimize while searching for the best possible network. However, we can also employ the MDL Score for explicitly rating the quality of a network.
Minimum Description Length
The Minimum Description Length (MDL) Score is a two-component score, which has to be minimized to obtain the best solution. It has been used traditionally in the artificial intelligence community for estimating the number of bits required for representing (1) a “model” and (2) “data given this model.”
In our machine-learning application, the “model” is a Bayesian network consisting of a graph and probability tables. The second term is the log-likelihood of the data given the model, which is inversely proportional to the probability of the observations (data) given the Bayesian network (model). More formally, we write this as:
- α represents BayesiaLab’s Structural Coefficient (the default value is 1), a parameter that permits changing the weight of the structural part of the MDL Score (the lower the value of α, the greater the complexity of the resulting networks),
- is the number of bits to represent the Bayesian network (graph and probabilities), and
- is the number of bits representing the dataset given the Bayesian network B (likelihood of the data given the Bayesian network).
The minimum value for the first term, , is obtained with the simplest structure, i.e., the fully unconnected network, in which all variables are stated as independent. The minimum value for the second term, , is obtained with the fully connected network, i.e., a network corresponding to the analytical form of the joint probability distribution, in which no structural independencies are stated.
Thus, minimizing this score consists of finding the best trade-off between both terms. For a learning algorithm that starts with an unconnected network, the objective is to add a link for representing a probabilistic relationship if, and only if, this relationship reduces the log-likelihood of the data, i.e., by a large enough amount to compensate for the increase in the size of the network representation, i.e., .
MDL Score Comparison
We now use the MDL Score to compare the results of all learning algorithms. We can look up the MDL Score of the current network by pressing W while hovering the cursor over the Graph Panel. This brings up an info box that reports a number of measures, including the MDL Score, which is displayed here as the “Final Score.”
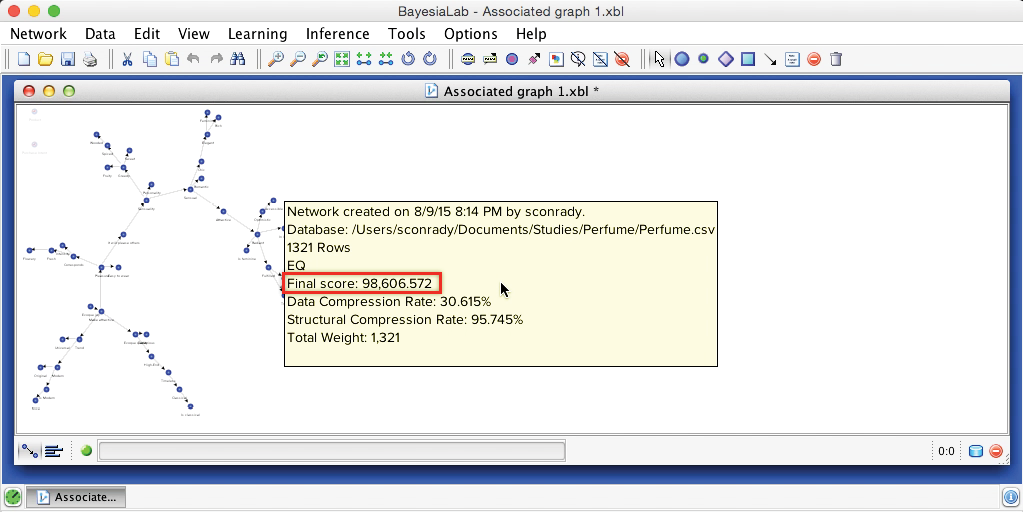
The MDL score can only be compared for networks with precisely the same representation of all variables, i.e., with the same discretization thresholds and the same data.
Alternatively, we can open up the Console via Menu > Options > Console > Open Console:
The Console maintains a kind of “log” that keeps track of the learning progress by recording the MDL Score (or “Network Score”) at each step of the learning process. Here, the “Final Score” marks the MDL Score of the current network, which is what we need to select the network with the lowest value.
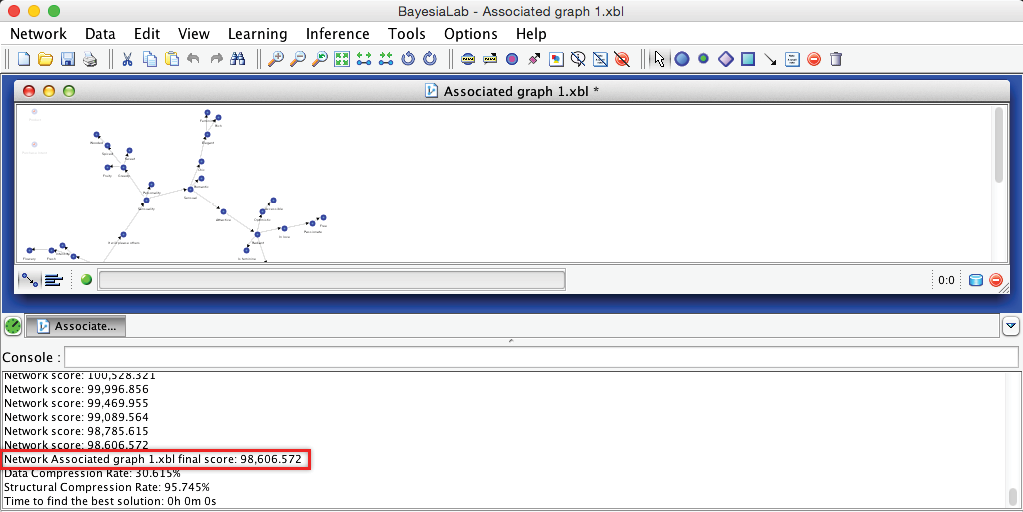
The EQ algorithm produces a network with an MDL Score of 98,606.572. As it turns out, this performance is on par with all the other algorithms we considered, although we skip presenting the details in this chapter. Given this result, we can proceed with the EQ-learned network to the next step.
Data Perturbation
As a further safeguard against utilizing a sub-optimal network, BayesiaLab offers Data Perturbation, which is an algorithm that adds random noise (from within the interval [-1,1]) to the weight of each observation in the dataset.
In the context of our learning task, Data Perturbation can help us escape from local minima, which we could have encountered during learning. We start this algorithm by selecting Learning > Data Perturbation.
For Data Perturbation, we need to set a number of parameters. The additive noise is always generated from a Normal distribution with a mean of 0, but we must set the Initial Standard Deviation. A Decay Factor defines the exponential attenuation of the standard deviation with each iteration.
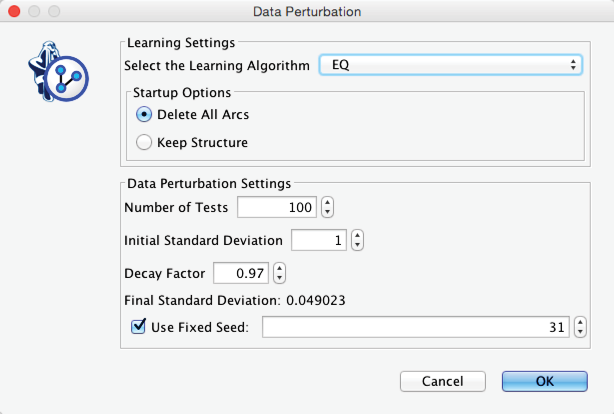
Upon completing Data Perturbation, we see the newly learned network in the Graph Panel. Once again, we can retrieve the score by pressing W while hovering with the cursor over the Graph Panel or by looking it up in the Console. The score remains unchanged at 98,606.572. We can now be reasonably confident that we have found the optimal network given the original choice of discretization, i.e., the most compact representation of the joint probability distribution defined by the 47 manifest variables.
On this basis, we now switch to the Validation Mode F5. Instead of examining individual nodes, however, we proceed directly to Variable Clustering.
