K-Means

Context

• K-Means is one of the Automatic Discretization algorithms for Continuous variables in Step 4 — Discretization and Aggregation of the Data Import Wizard.

Algorithm Details & Recommendations

• The K-Means algorithm is based on the classical K-Means data clustering algorithm but uses only one dimension, which is the to-be-discretized variable.

• K-Means returns a discretization that directly depends on the Probability Density Function of the variable.

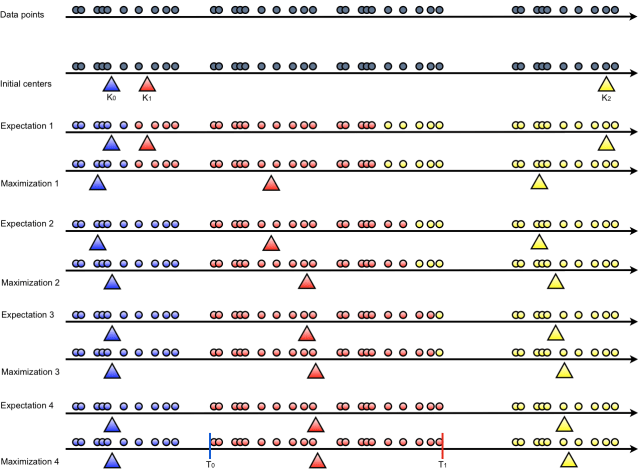
• More specifically, it employs the Expectation-Maximization algorithm with the following steps:

  1. Initialization: random creation of K centers
  2. Expectation: each point is associated with the closest center
  3. Maximization: each center position is computed as the barycenter of its associated points

• Steps 2 and 3 are repeated until convergence is reached.

• Based on the centers K, the discretization thresholds are defined as:

• The following figure illustrates how the algorithm works with K=3.

• For example, applying a three-bin K-Means Discretization to a normally distributed variable would create a central bin representing 50% of the data points and one bin of 25% each for the distribution’s tails.
• Without a Target variable, or if little else is known about the variation domain and distribution of the Continuous variables, K-Means is recommended as the default method.