The Birth-Weight Paradox
Context
"In the mid-1960s, Jacob Yerushalmy pointed out that a mother’s smoking during pregnancy seemed to benefit the health of her newborn baby, if the baby happened to be born underweight."
Pearl, Judea. The Book of Why: The New Science of Cause and Effect (p. 183). Basic Books. Kindle Edition.
The Paradox Illustrated
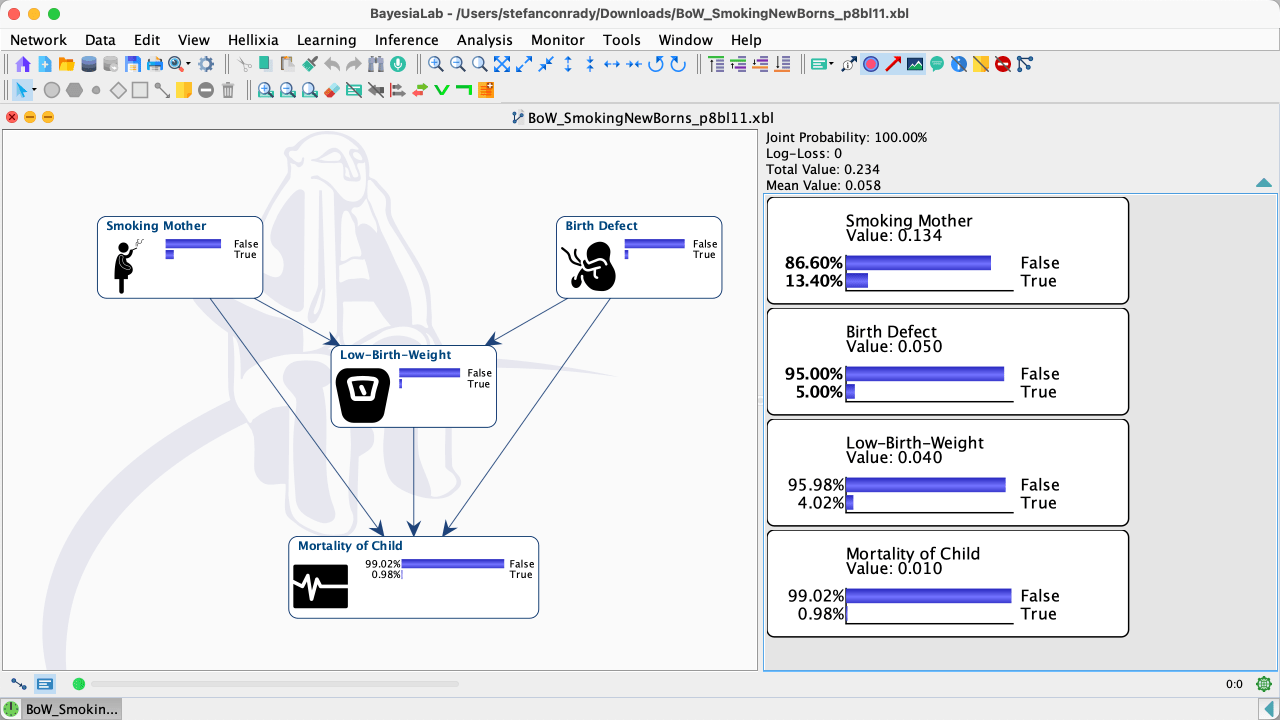
We implemented this counterintuitive example as a causal Bayesian network, which means the arcs represent causal relationships.
Since the problem's description in the book is purely qualitative, and no data is available, we associated arbitrary probability distributions with the nodes. Although arbitrary, we specified the probabilities so that the network produces the paradoxical behavior described by Pearl.
You can download this Bayesian network in XBL format and open it with any version of BayesiaLab:
BoW_SmokingNewBorns.xbl
30 KB
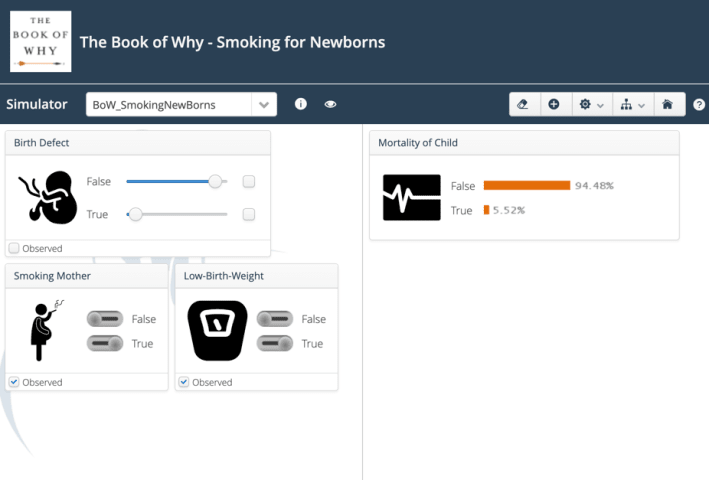
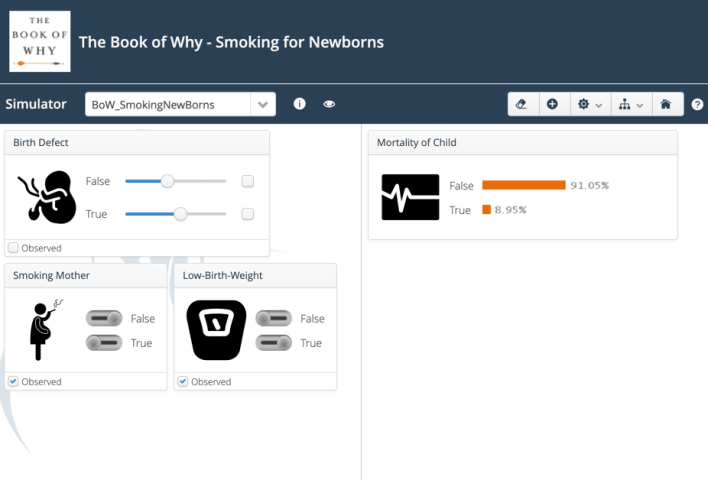
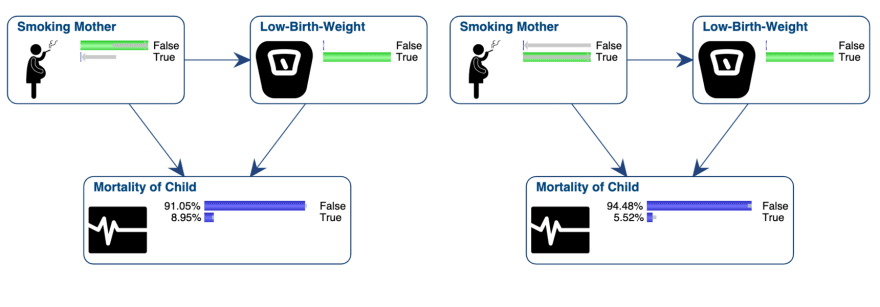
The birth-weight paradox can be highlighted with two observations:
- Babies of smokers have a lower birth weight than babies of non-smokers.
- Low-birth-weight babies of smoking mothers have a higher survival rate compared to those of non-smokers.
The Paradox Resolved
"Smoking may be harmful in that it contributes to low birth weight, but certain other causes of low birth weight, such as serious or life-threatening genetic abnormalities, are much more harmful. There are two possible explanations for low birth weight in one particular baby: it might have a smoking mother, or it might be affected by one of those other causes." (Pearl, pp. 184–185)
In other words, is a collider in the structure
By observing , we open a noncausal ("back-door") path between and , which gives rise to the paradox. Please see our discussion of the Back-Door Criterion for more details on noncausal paths.
In BayesiaLab, we can illustrate what happens by highlighting all information paths:
-
Set as Target Node.
-
Set evidence on .
-
Select . Then, run
Menu > Analysis > Visual > Graph > Influence Paths to Target. -
Now, all influence paths are visible.
-
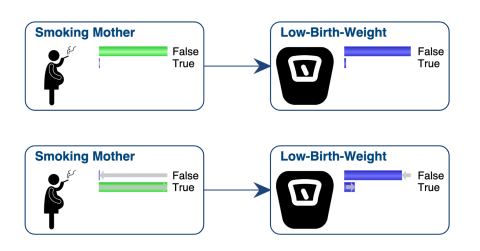
If we observe , this explains away and reduces the probability of ;
-
On the other hand, if we observe , the probability of increases, and the probability of increases, too.
- Alternatively, we can use the WebSimulator (opens in a new tab) to replicate these two scenarios:
