Network Performance Analysis: Target — Gains Curve
When one is faced to the problem of predicting the value of a particular variable (the value of the target node), the evaluation of the model can be realized by using the gain curve.
The Gains Curve is generated by sorting, in decreasing order, the individuals according to the target value probability returned by the network, e.g. the fraud or churn probability. The X-axis represents the rate of individuals that are taken into account. The Y-axis represents the rate of individuals with the target value that have been identified as such.
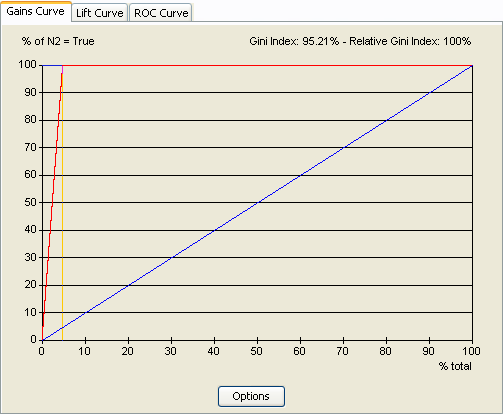
In the Gains Curve below, there are almost 5% of individuals that have the target value (yellow). The blue curve represents the gain curve of a pure random policy, i.e. choosing the individuals without any order. The red curve represents the gain curve corresponding to the optimal policy, i.e. where the individuals are sorted according to the perfect model. Choosing the first 5% of individuals allows then getting 100% of the individuals with the target variable with the optimal policy, against only 5% with the random policy.
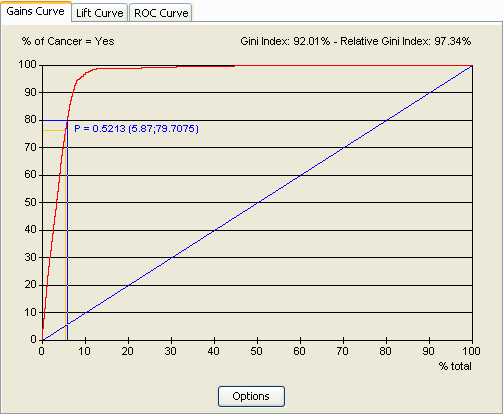
A left click on the curve shows exact coordinates of the corresponding point and the probability of the target value of the associated case.
For example, the screenshot below indicates that the selection of the first 5.87% cases imply a detection rate of 79.71%. It also indicates that the last case of that selection has a probability of having the target value equals to 52.13%.
The Gini Index and the Relative Gini Index are computed according to the curve and displayed at the top of the graphic. The Gini Index is computed as the surface under the red curve and above the blue curve divided by the surface above the blue curve. But, as shown above, the surface of the optimal policy is less than the surface above the blue line, so the relative Gini index is computed as the surface under the red curve and above the blue curve divided by the surface under the curve of the optimal policy and above the blue curve. It is a more representative coefficient.
This interactive curve is not only an evaluation tool. It is also a decision support tool that allows defining the best probability threshold from which an individual will be considered as belonging to the target.
A right click on the graphical zone allows choosing between printing the curve and copying it to the clipboard. In the last case, it is then possible to paste it directly as an image, or to paste the corresponding data points.
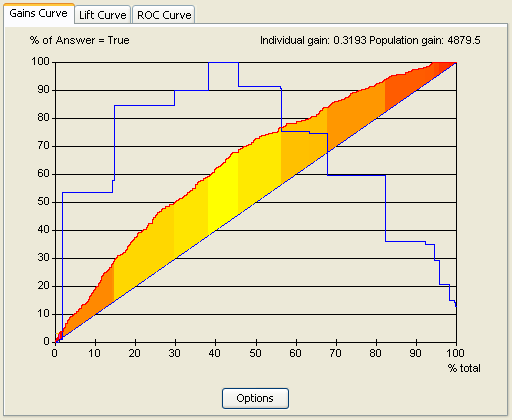
The gain curve has a tool used to automatically analyze the expected economical gains with the evaluated model. These computations follow the definition of the unit costs corresponding to the treatment of each individual (x-axis), of unit gains corresponding to each positive answer (y-axis), and finally of a target population’s size. The economical gain is then defined as the difference between the profit corresponding to the treatment of x% of the population and the profit corresponding to the treatment of the whole pop- ulation. As the following screen captures shows it, the result is displayed as a curve (blue curve) and as a gradient of color (the closer we are to the yellow, the more we are close to optimality).
The economical parameters can be modified with the following dialog: