Mutual Information

The Mutual Information $I(X, Y)$ measures the amount of information gained on variable $X$ (the reduction in the Expected Log-Loss) by observing variable $Y$:

The Venn Diagram below illustrates this concept:

The Conditional Entropy $H(X|Y)$ measures, in bits, the Expected Log-Loss associated with variable $X$ once we have information on variable $Y$:

Hence, the Conditional Entropy is a key element in defining the Mutual Information between $X$ and $Y$.

Note that

is equivalent to:

and furthermore equivalent to:

This allows computing the Mutual Information between any two variables.

Usage

For a given network, BayesiaLab can report the Mutual Information in several contexts:

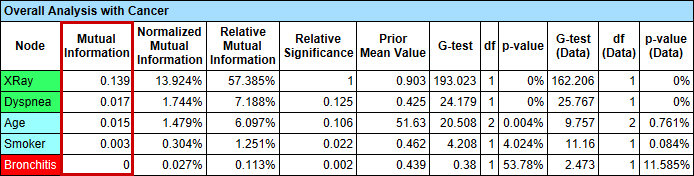
• Menu > Analysis > Report > Target > Relationship with Target Node.
• Note that this table shows the Mutual Information of each node, e.g., XRay, Dyspnea, etc., only with regard to the Target Node, Cancer.

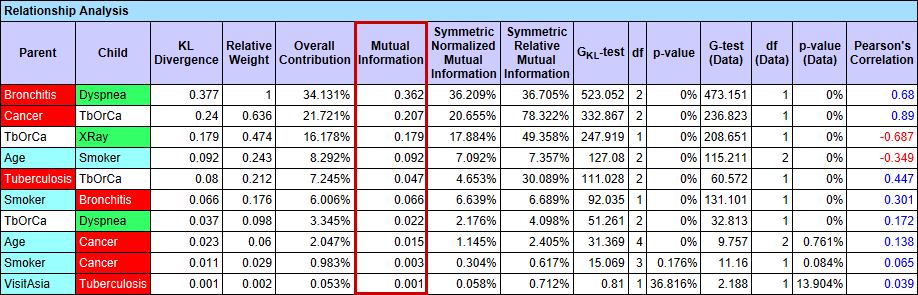
• Menu > Analysis > Report > Relationship Analysis:

• The Mutual Information can also be shown by selecting Menu > Analysis > Visual > Overall > Arc > Mutual Information and then clicking the Show Arc Comments icon or selecting Menu > View > Show Arc Comments.

• Note that the corresponding options under Preferences > Analysis > Visual Analysis > Arc's Mutual Information Analysis have to be selected first:

• In Preferences, Child refers to the Relative Mutual Information from the Parent onto the Child node, i.e., in the direction of the arc.
• Conversely, Parent refers to the Relative Mutual Information from the Child onto the Parent node, i.e., in the opposite direction of the arc.