Context

• This feature compares a segment to a selected benchmark, such as (either the entire data set or another segment).

• The comparison is done in terms of Impacts, a term combining the difference of the observable variables' mean values and their effect on the Target Node.

• The Impact $I$ for each observable variable $V$ is computed as follows: where:

  • $s$ is the analyzed segment,
  • $b$ is the benchmark,
  • $\bar v_s$ is the mean value of ${V}$ of the data defined by the segment, $\bar v_b$ is the mean value of ${V}$ of the data defined by the benchmark.
  • $E_b^V$ is the effect of ${V}$ on the Target Node, evaluated on the benchmark.

• Four types of effects can be calculated:

  • Total Effect
  • Standardized Total Effect
  • Direct Effect
  • Standardized Direct Effect

Example

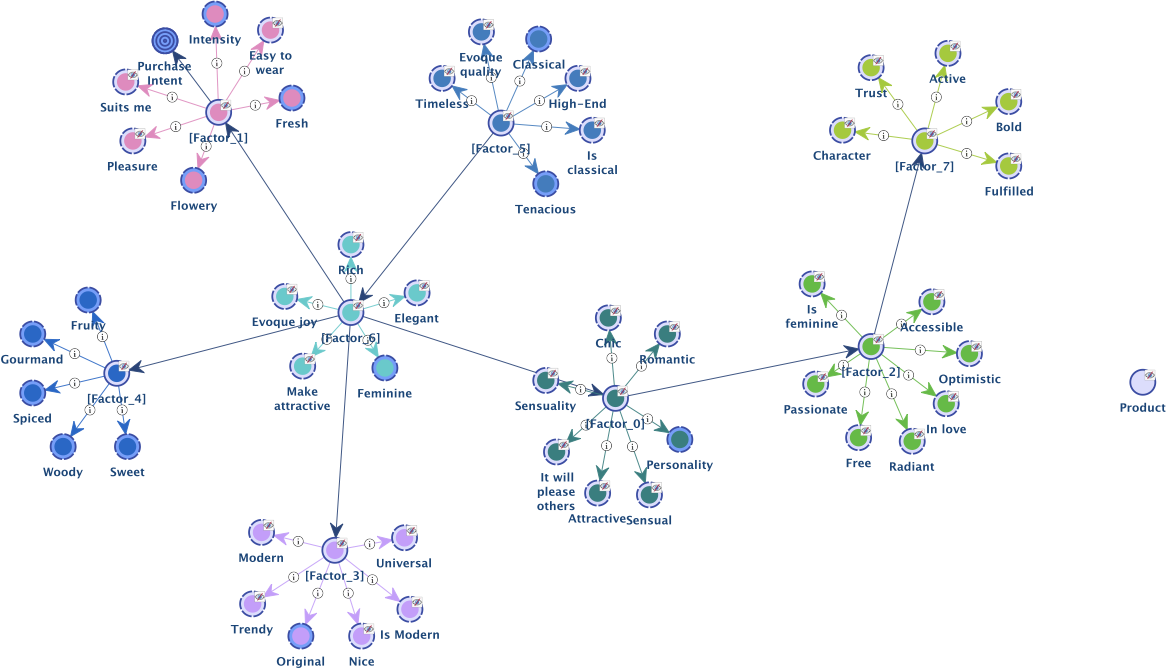
• Let's take the Perfume example for which we have defined five segments with the Breakout Variable Product, namely Prod3, Prod4, ProdG1, ProdG5 and Prod G6.

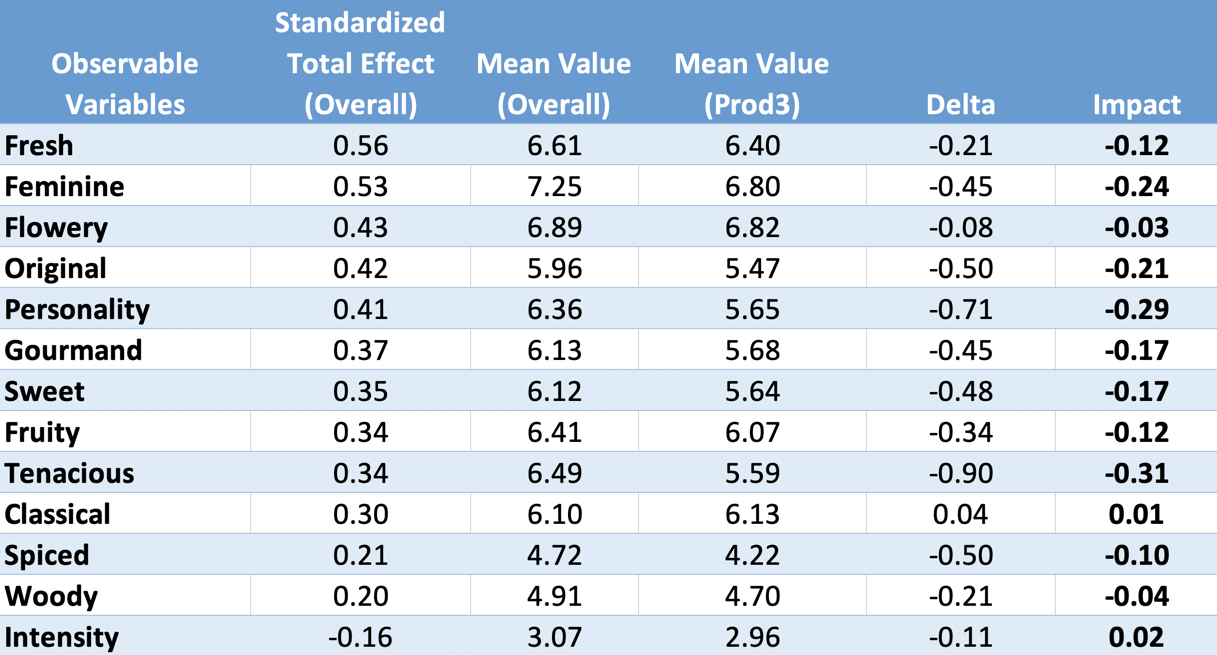
Below is the table with the Standardized Total Effects of all the observable variables on Purchase Intent, and the mean values of these variables, computed on the entire data set, and on the segment represented by Prod3. These figures allows computing the Impacts of each variable.

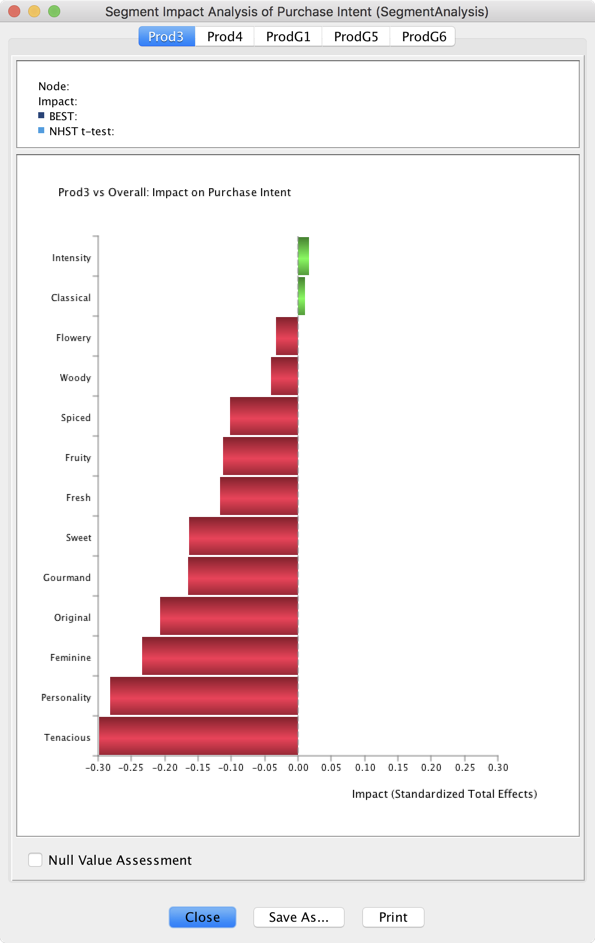
Null Value Assessment

• This option allows estimating if the segment and benchmark mean values are significantly different. Two tests are proposed for answering this question:

  • a Frequentist one, NHST t-test, the Null Hypothesis Significance Testing with the Welch's two-sample, two tailed t-test, and
  • a Bayesian one, BEST, described in the paper by John K. Kruschke, "Bayesian Estimation Supersedes the t-test", Journal of Experimental Psychology: General, 2013.

• Below is the Bayesian network used in the BEST approach. We are assuming that the samples follow a Student's t-distribution.

• The segment and the benchmark have their own $/mu$ and $/sigma$, but they share the same $/nu$.

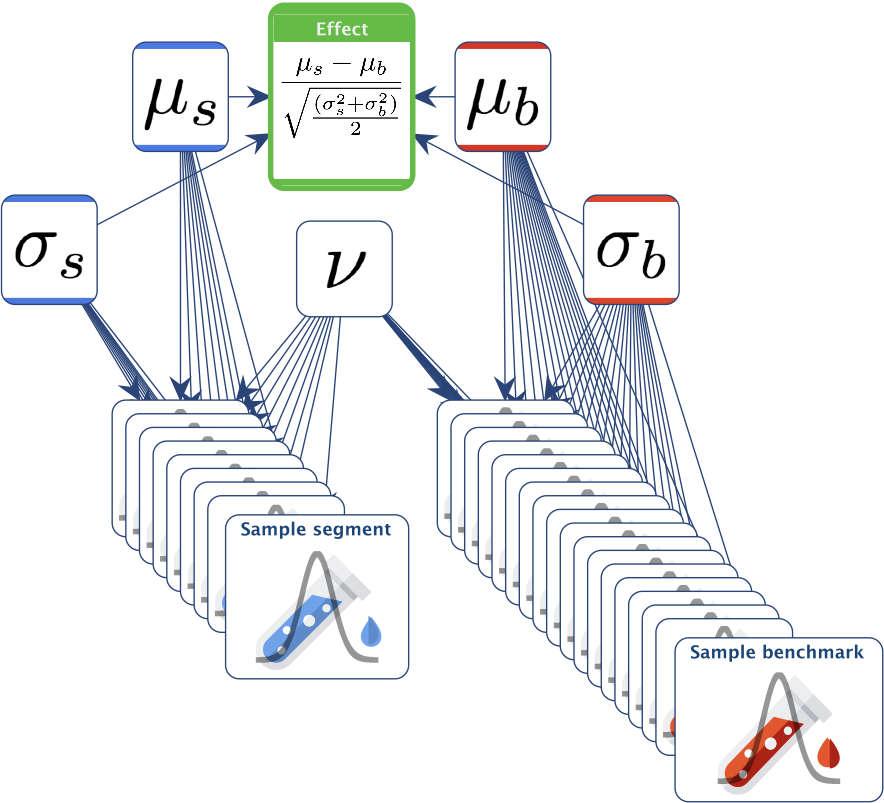
• The default Confidence Level has been set to 95%. This is the same for both tests.
• As for the Bayesian test, the Region of Practical Equivalence (ROPE) on the Effect size around the null value has been set by default to [-0.1, 0.1].
• The null value is declared to be rejected if the 95% Highest Density Interval (HDI) falls completely outside the ROPE.
• Under Menu > Window > Preferences you can modify:
  • the confidence level (for both the t-test and BEST),
  • the Monte Carlo Markov Chain parameters that are used for inference in the Bayesian network described above,
  • the ROPE size that defines an interval centered at 0, i.e. 0.2 defines the interval [-0.1, 0.1].

Example

• Checking Null Value Assessment triggers the computation of both tests.

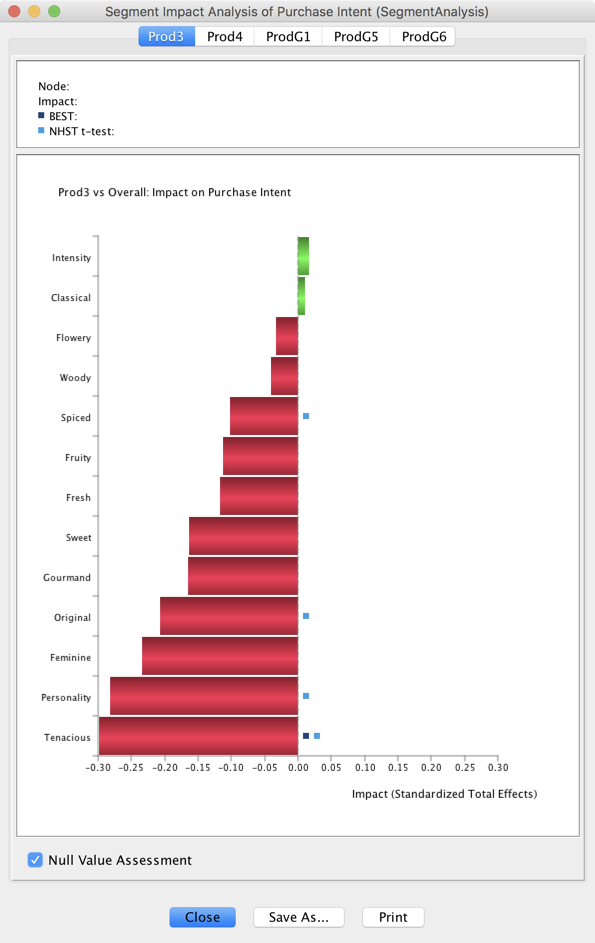
• If the mean values are estimated as significantly different, a square is added next to the Impact bar:
  • for t-test
  • for BEST