Edit Structural Priors (9.0)

Overview & Context

• If expert knowledge is available prior to machine-learning a network structure from data, it can be useful to incorporate such knowledge into the learning process to improve the quality of the model to be learned.
• BayesiaLab offers various methods for specifying prior knowledge:
  • Structural Constraints
  • Dirichlet Priors
  • Structural Coefficient

Structural Constraints

• Structural Constraints are priors that bias the learning of the network structure, but not the estimation of the probabilities.
• There are three ways to define this type of prior:
  • Fixed Arcs — After defining Fixed Arcs, certain unsupervised structural learning algorithms, i.e., EQ, TabooEQ, and Taboo, upon startup, allow you to select Delete Unfixed Arcs or Keep Structure, which results in keeping the fixed arcs in place, even though the underlying data may not support these fixed relationships. ​
  • Forbidden Arcs — If you formally define arcs as forbidden, they will not be added to a network by any structural learning algorithm.
  • Temporal Indices — In structural learning, a node cannot become the ancestor of a node that has a lower temporal index, i.e., is earlier in time.

Dirichlet Priors

• Dirichlet Priors can be considered as virtual particles sampled from a fully-specified Bayesian network that represents expert knowledge.
• There are also three ways to define this type of prior:
  • Uniform Prior Samples (Smoothed Probability Estimation) are particles sampled from a joint probability distribution that is defined by an entirely unconnected Bayesian network in which all nodes have a uniform distribution of states. This so-called uninformative prior specifies that "everything is possible", i.e., it prevents having zero probabilities in any of the Conditional Probability Tables. While such Uniform Priors primarily bias the estimation of probabilities,  they can also have an impact on the machine-learned network structure.
  • Prior Samples are "virtual" particles sampled from a fully-specified Bayesian network that represents prior knowledge. The "virtual" particles are then augmented with "actual" particles from a dataset associated with the Bayesian network. As a result, BayesiaLab's learning algorithms will learn from the merged set of "virtual" and "actual" particles to discover the network structure and estimate the parameters.
  • Parameter Updating — while the first two methods define static priors (uninformative or based on a fully-specified Bayesian network), the priors in Parameter Updating evolve as the current Bayesian network parameters are updated.

Structural Coefficient

• Structural Coefficient — all of BayesiaLab's structural learning algorithms use the Minimum Description Length (MDL) score to evaluate the quality of a network given its associated data set.
  • Minimizing the MDL Score is approximatively equivalent to maximizing the a posteriori of the network given the data.
  • It is approximate because the priors of the network are approximated with a heuristic that assigns them a probability that is inversely proportional to the complexity of the network.
  • By default, both the prior and the likelihood terms have the same weight, which is rather conservative.
  • There are two ways to change the weight of the heuristic used for approximating the priors:
    • Overall Structural Coefficient (values between 0 and 150): you can modify the number of particles utilized during structural learning by defining a weight for each particle that is inversely proportional to the Overall Structural Coefficient.
      • Choosing a value of less than 1 is equivalent to increasing the number of particles and therefore increases the sensitivity of the learning algorithms, resulting in more complex structures.
      • Choosing a value greater than 1 is equivalent to reducing the number of particles and thus decreases the sensitivity of the learning algorithms, resulting in simpler network structures.
      • In other words, the Overall Structural Coefficient permits you to modify the "significance threshold" for detecting relationships between nodes.
    • Local Structural Coefficients: the MDL score is decomposable, which means that the score of the network is equal to the sum of the MDL scores of the nodes.
      • A Local Structural Coefficient of less than 1 decreases the cost of adding incoming arcs to the associated node.
      • A Local Structural Coefficient of greater than 1 increases the cost of adding incoming arcs to the associated node.

New Feature: Structural Priors

• As of version 9.0, prior knowledge can now be defined at the arc level, i.e., "more locally" than what is possible with Local Structural Coefficients, which operate at the node level.

• a Structural Priors Editor allows you to manage Structural Priors at the arc level.

  

Usage

• You can open the Structural Priors Editor in two ways:

  • Select Edit > Edit Structural Priors from BayesiaLab's Main Menu.
  • Right-click on the Graph Panel background to open the Contextual Menu and select Edit Structural Priors.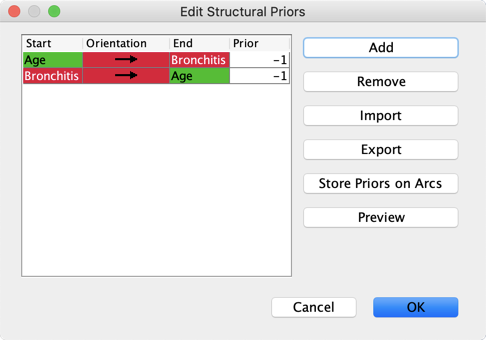
  

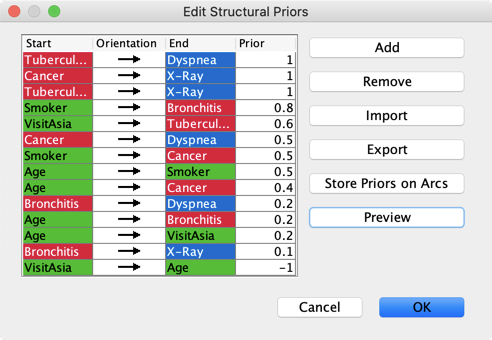
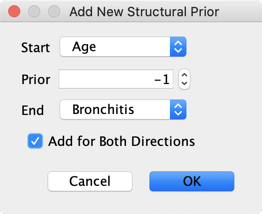
• To add a Structural Prior, click the Add button, specify the Start node, the End node, and the value of the Prior.

  • The values of Structural Priors can range between -1.0 and 1.0.
  • -1.0 strongly increases the cost of adding an arc, and 1.0 strongly reduces it.
    • However, -1.0 is not the same as forbidding the arc in the Forbidden Arc Editor. If the data suggests a strong relationship between the relevant nodes, an arc can still be added between them.
    • Also, +1.0 does not mean forcing the arc. If the data suggests that the relationship between nodes is weak, no arc will be added.
  • Additionally, you can check the box Add for Both Directions to apply the same Structural Prior value for both arc directions.
  

• By clicking on a column header in the Structural Priors Editor, you can sort the table by that column.

• The color of the Orientation cell is identical for those arcs that have the same Structural Prior assigned to both arc directions.

  

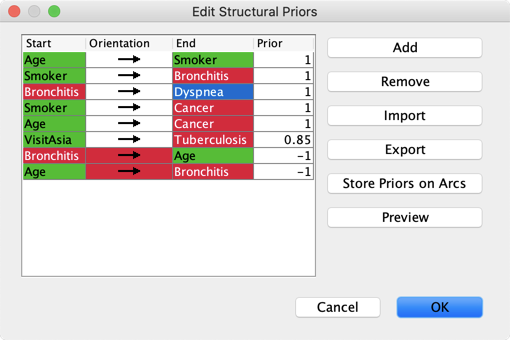
Import Export Dictionaries of Structural Priors

• You can use Dictionaries to save and load Structural Priors. Structural Priors Dictionaries.

Store Priors on Arcs

• Clicking the Store Priors on Arcs button adds the value of the Structural Prior as an Arc Comment.

• Once your network is learned, and you click the Show Arc Comments button  in the Menu Bar, the Structural Prior appears as a badge on the corresponding arc.

  

• Note that this is a one-time copy & paste of values into the Arc Comment field, which is not updated if you later change a Structural Priors or even change an arc direction manually. The Arc Comment remains unchanged until you click Store Priors on Arcs again.

Preview

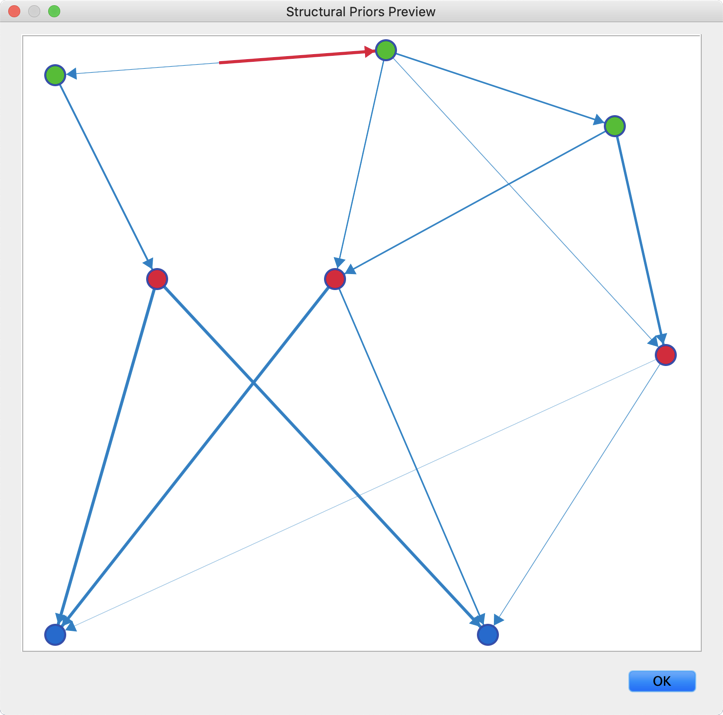
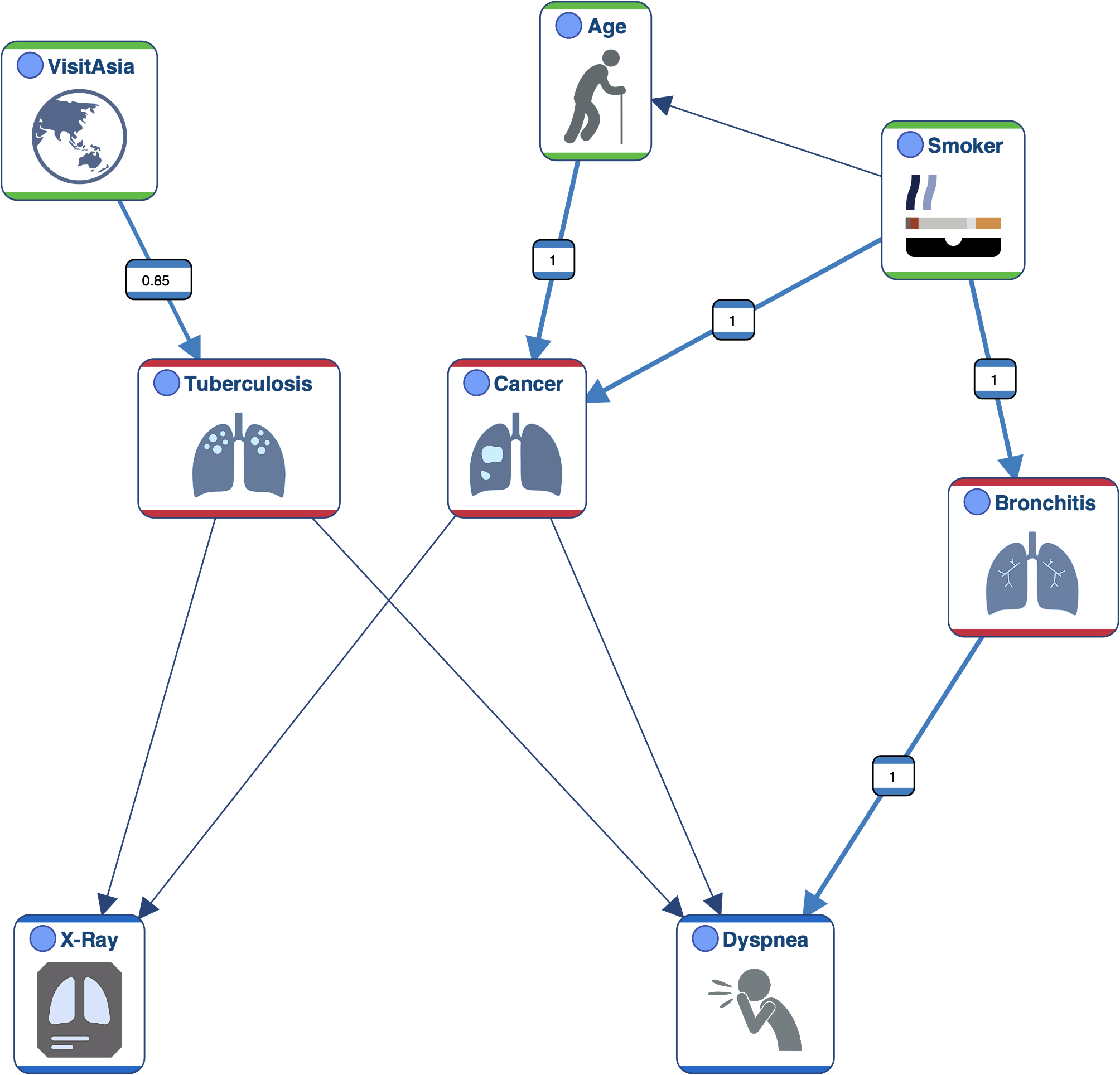
• Clicking the Preview button generates a visualization of the Structural Priors you have defined.

• The thickness of the links is proportional to the absolute value of the respective Structural Priors.

• Positive Structural Priors are represented in blue, negative Structural Priors are shown in red.

• If the Structural Priors are different for each direction, the thickness and color attributes are applied to half-arcs so both directions can be shown.