Partial Order Learning (9.0)
Context
Learning | Partial Order Learning
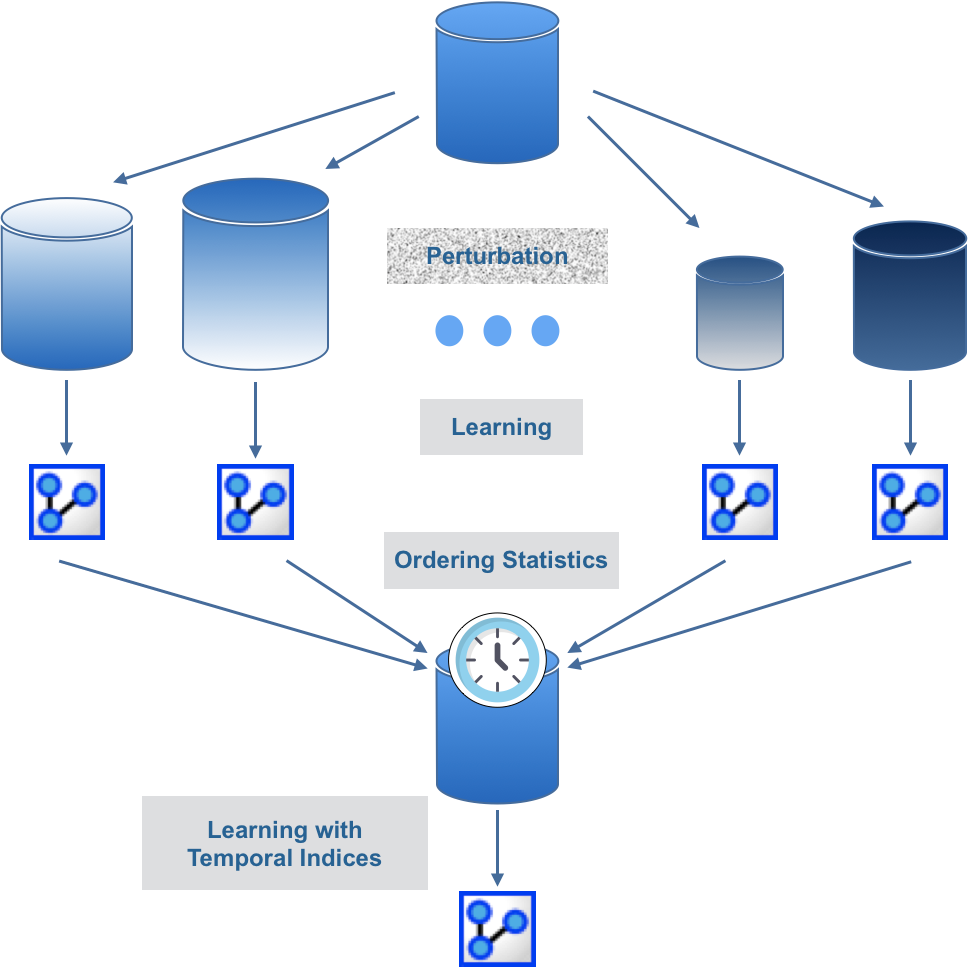
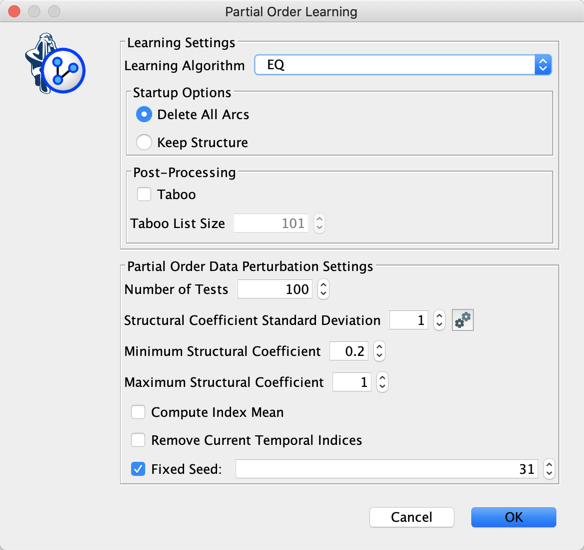
The Partial Order Learning is a Meta-Learning algorithm that can be compared to Bagging. It is based on Data Perturbation (Smoothed Bootstrapping) for learning a set of networks that are transformed into Essential Graphs to define a set of Partial Orderings.
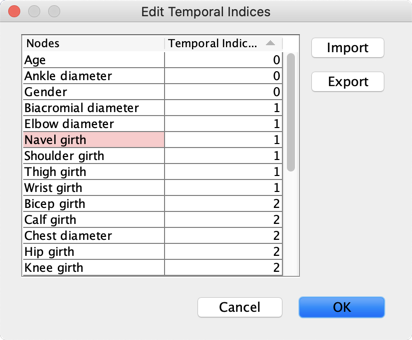
In a Partial Ordering, the index of a node is incremented only when it has parents in the Essential Graph. The indices of a Partial Ordering are saved as Temporal Indices.
There are 2 options for summarizing the node indices that have been estimated on the bag of networks:
- The mean value (a real value),
- A vote (an integer).
Once defined, the Temporal Indices are used for learning a network on the original unperturbed data set.
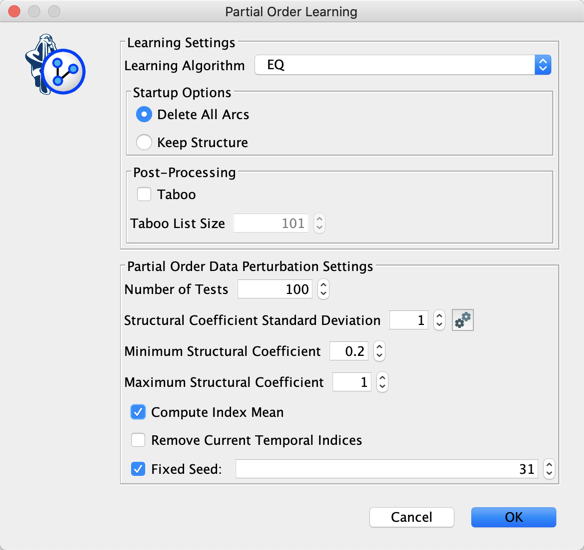
Example
Let’s use the example we used for illustrating Structural Prior Learning.
We keep the structural priors that have been estimated and we compare the 2 options for summarizing the indices.
- Mean Value
- Vote
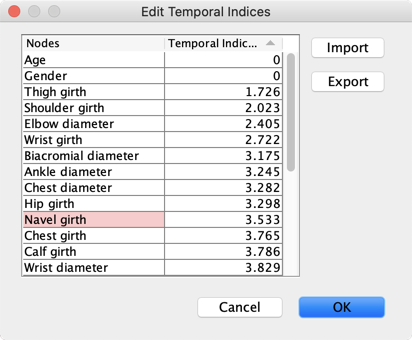
We uncheck Remove Current Temporal Indices to keep our initial temporal indices that define Age and Gender as root nodes.
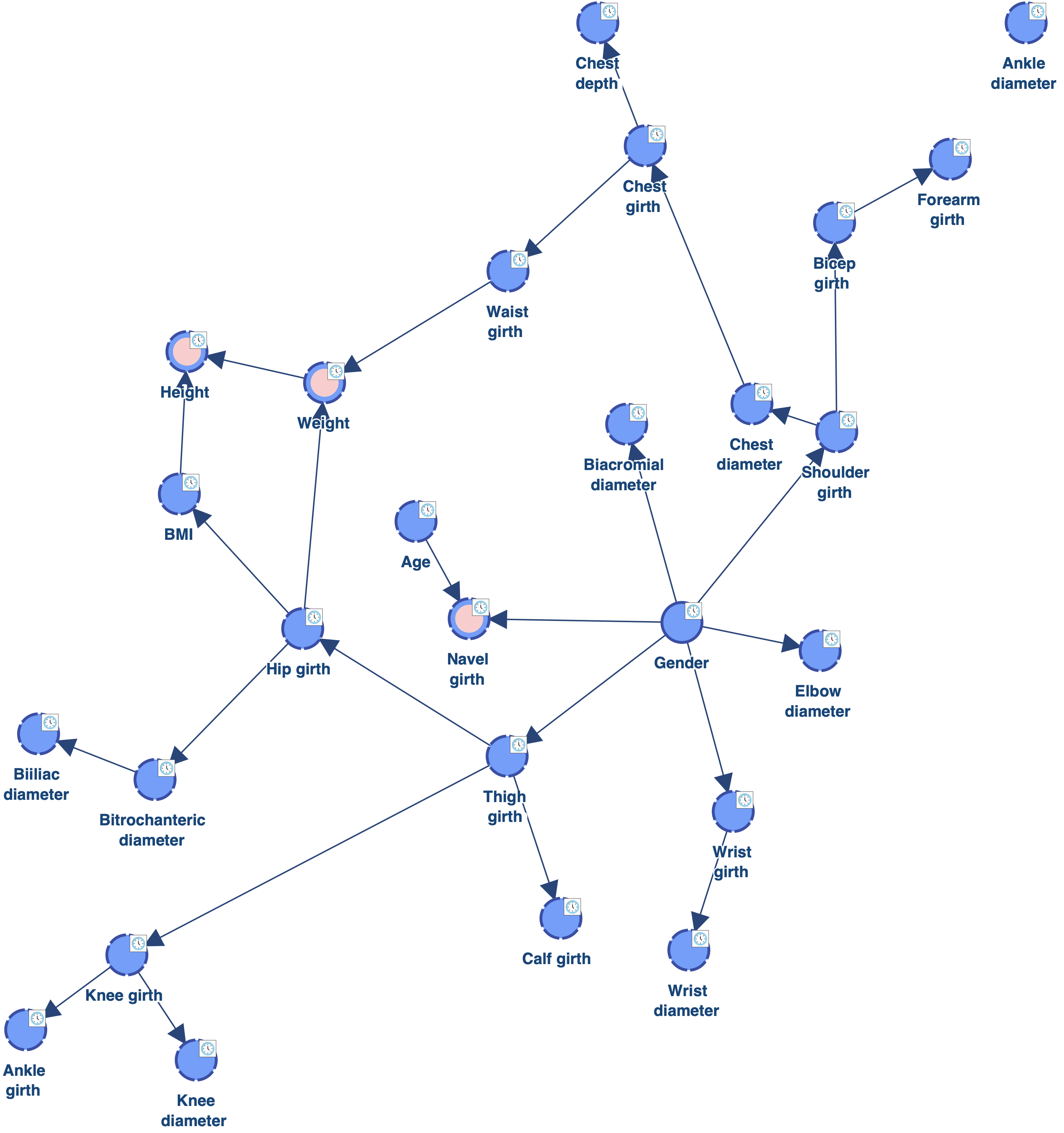

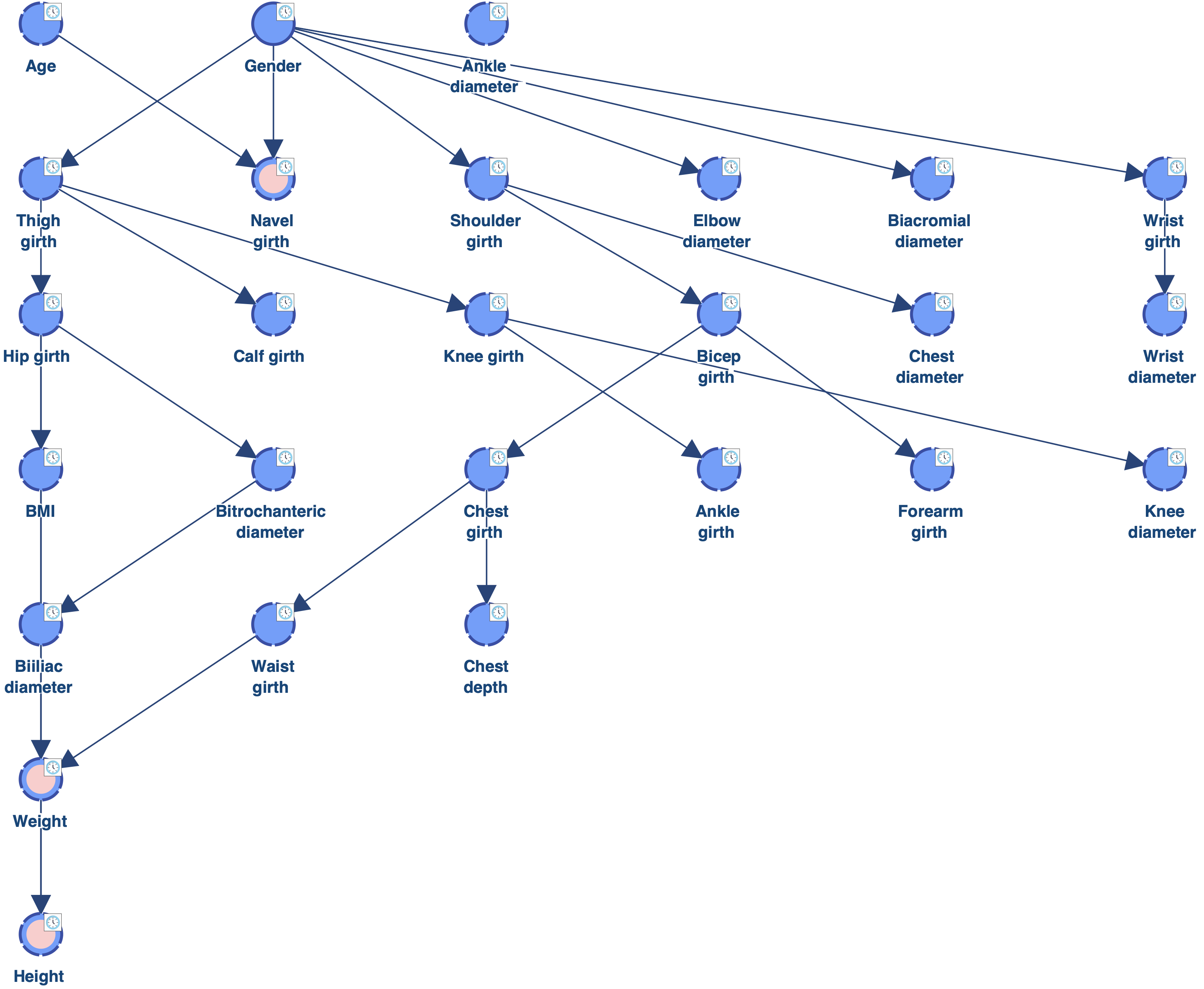
Below is the layout we get by using the new Temporal Index Layout.

Temporal indices computed as mean values return information that can be useful, but it can also be misleading. Indeed, it is possible to have mean indices that have never been found in any network (e.g. a mean index equal to 3 with two indices equal to 1 and 5). This is the reason why it probably safer to use the Vote instead.
We uncheck Remove Current Temporal Indices to keep our initial temporal indices that define Age and Gender as root nodes.
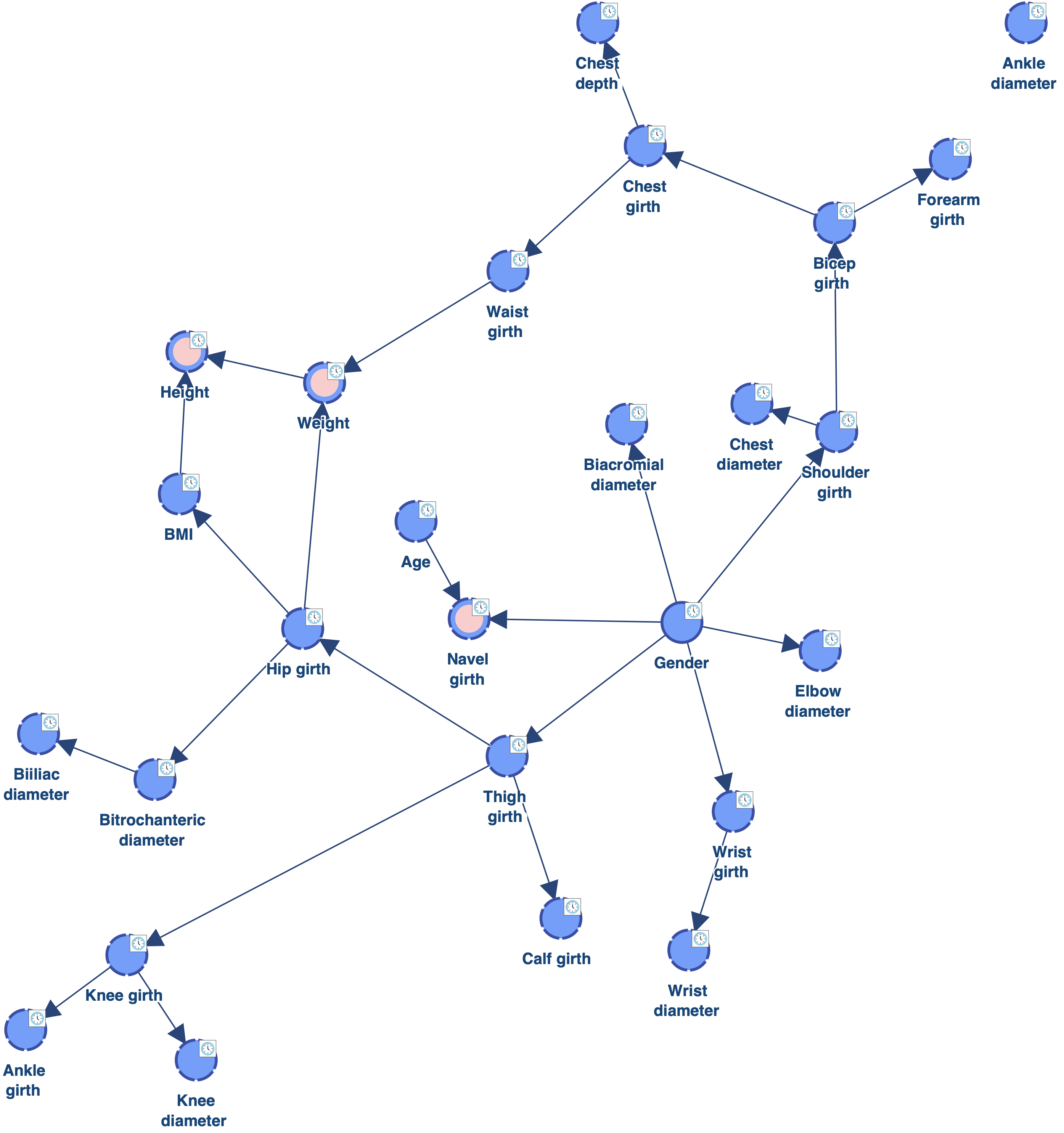

The graph below shows the layout we get by using the new Alignment function that uses Temporal Indices.