Discrete Probability Distributions
NoisyOr(s, leak, c1, p1, cn, pn)
Description: This function represents a noisy Or in which the effect of the parents (the causes ci) on the symptom s can be inhibited. pi represents the probability that the cause i acts on the symptom (the inhibition probability is then 1-pi). It is also possible to define a leak probability for the set of causes that are not directly modeled.
- Number of Parameters: even, and >= 4
- Parameter Type: boolean, numerical, boolean, numerical, ..., boolean, numerical
- Result Type: real
The conditional probability table below corresponds to NoisyOr(?N3?, 0.1, ?N1?, 0.8, ?N2?, 0.6):
| N1 | N2 | N3 = False | N3 = True |
|---|---|---|---|
| False | False | (1-0.1) | 0.1 |
| False | True | (1-0.1) * (1-0.6) | 0.64 |
| True | False | (1-0.1) * (1-0.8) | 0.82 |
| True | True | (1-0.1) _ (1-0.8) _ (1-0.6) | 0.928 |
NoisyAnd(s, leak, c1, p1, cn, pn)
Description: This function represents a noisy And, i.e., the Noisy Or negation.
- Number of Parameters: even, and >= 4
- Parameter Type: boolean, numerical, boolean, numerical, ..., boolean, numerical
- Result Type: real
The conditional probability table below corresponds to NoisyAnd(?N3?, 0.1, ?N1?, 0.8, ?N2?, 0.6):
| N1 | N2 | N3 = False | N3 = True |
|---|---|---|---|
| False | False | 0.928 | (1-0.1) _ (1-0.6) _ (1-0.8) |
| False | True | 0.82 | (1-0.1) * (1-0.8) |
| True | False | 0.64 | (1-0.1) * (1-0.6) |
| True | True | 0.1 | (1-0.1) |
Binomial(k, n, p)
Description: Probability of obtaining exactly k occurrences of the same event of probability p among n independent experiments.
- Number of Parameters: 3
- Parameter Type: integer, integer, numerical
- Result Type: real
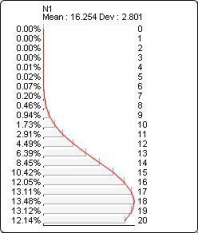
The probability distribution below corresponds to Binomial(?N1?, 20, 0.3):
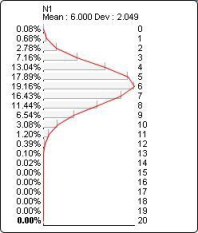
NegBinomial(k, n, p)
Description: Probability of requiring k trials to have n successes of the same event of probability p among independent experiments.
- Number of Parameters: 3
- Parameter Type: integer, integer, numerical
- Result Type: real
The probability distribution below corresponds to NegBinomial(?N1?, 4, 0.3):
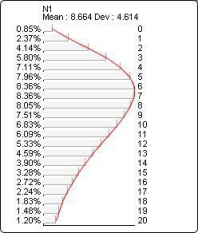
Geometric(k, p)
Description: Probability of requiring k independent experiments to obtain a first observation of an event of probability p.
- Number of Parameters: 2
- Parameter Type: integer, numerical
- Result Type: real
The probability distribution below corresponds to Geometric(?N1?, 0.3):
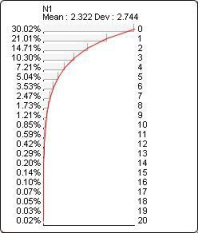
Hypergeometric(k, n, m, N)
Description: Probability of obtaining k winning objects when choosing n objects among N, where m are winning objects.
- Number of Parameters: 4
- Parameter Type: integer, integer, integer, integer
- Result Type: real
The probability distribution below corresponds to Hypergeometric(?N1?, 5, 5, 20):
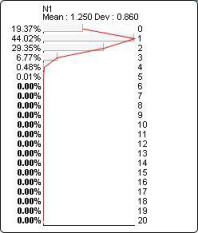
Poisson(k, l)
Description: Probability of obtaining k observations of an event in a large number of independent experiments when the mean is l.
- Number of Parameters: 2
- Parameter Type: integer, real
- Result Type: real
The probability distribution below corresponds to Poisson(?N1?, 18.5):
DiscUniform(k, a, b)
Description: Uniform distribution defined by the discrete interval [a, b].
- Number of Parameters: 3
- Parameter Type: integer, integer, integer
- Result Type: real