Profile Analysis
Context
- The Profile Analysis feature allows you to compare the mean values of observable variables on the segments defined by the Breakout variable.
Example
- Let’s take the Perfume example for which we have defined five segments with the Breakout Variable Product, namely Prod3, Prod4, ProdG1, ProdG5 and Prod G6.
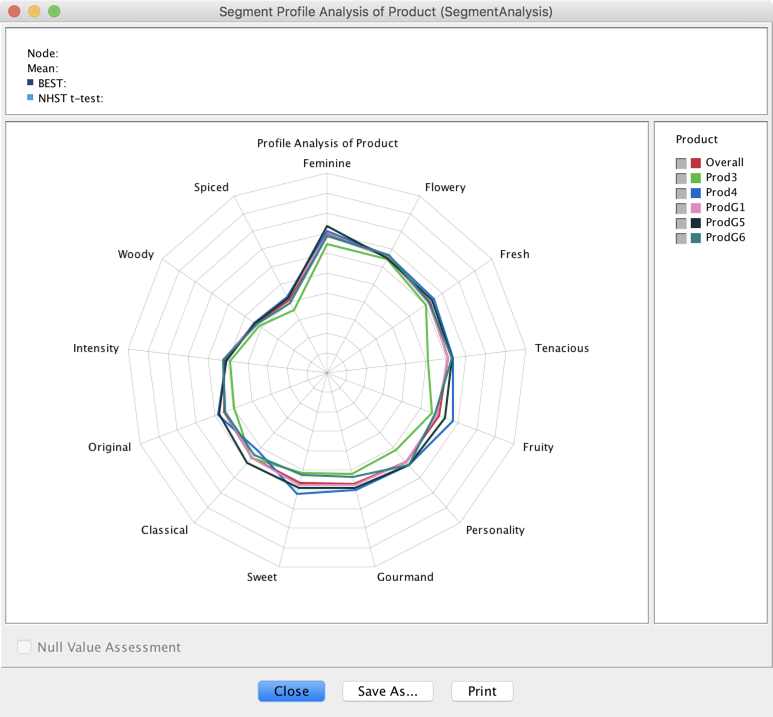
Null Value Assessment
-
When two segments are selected, this option allows estimating if the mean values of these segments are significantly different.
-
Two tests are proposed for answering this question:
- a Frequentist one, NHST t-test, the Null Hypothesis Significance Testing with the Welch’s two-sample, two tailed t-test, and
- a Bayesian one, BEST, described in the paper by John K. Kruschke, “Bayesian Estimation Supersedes the t-test”, Journal of Experimental Psychology: General, 2013.
-
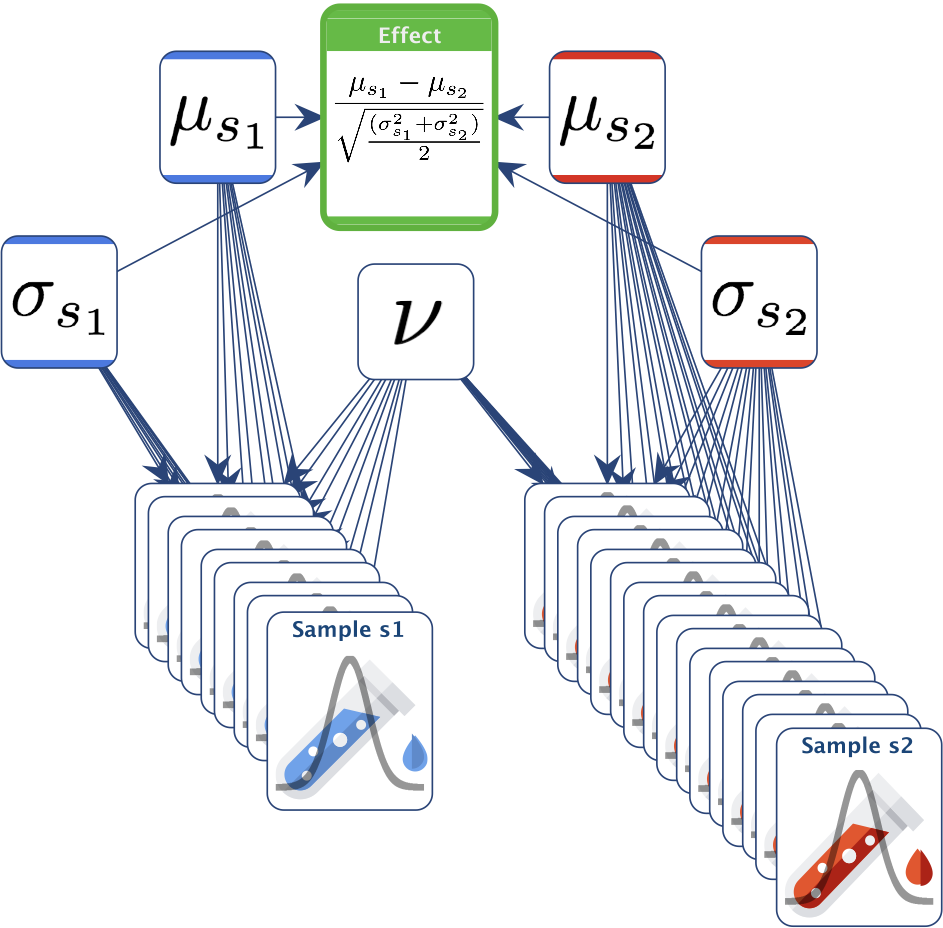
Below is the Bayesian network used in the BEST approach. We are assuming that the samples follow a Student’s t-distribution. The two segments have their own and , but they share the same .
-
The default Confidence Level has been set to 95%. This is the same for both tests.
-
As for the Bayesian test, the Region of Practical Equivalence (ROPE) on the Effect size around the null value has been set by default to [-0.1, 0.1].
-
The null value is declared to be rejected if the 95% Highest Density Interval (HDI) falls completely outside the ROPE.
-
You can use the Preferences to modify:
- the confidence level (for both the t-test and BEST),
- the Monte Carlo Markov Chain parameters that are used for inference in the Bayesian network described above,
- the ROPE size that defines an interval centered at 0, i.e. 0.2 defines the interval [-0.1, 0.1].
Example
-
We first select Prod3 and ProdG5. Upon checking Null Value Assessment, the computation of both tests is triggered.
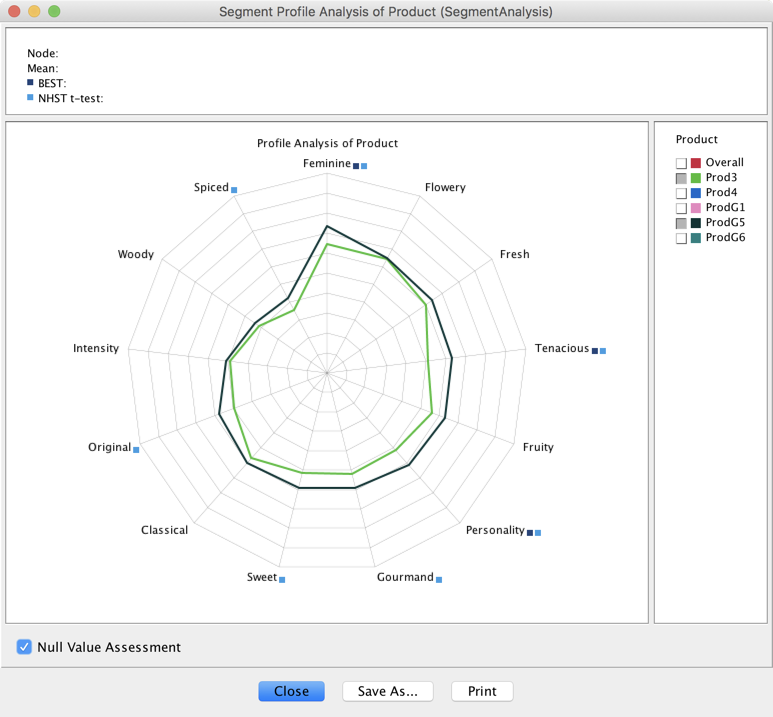
-
If the mean values are estimated as significantly different, a square is added next to the label:
 for t-test
for t-test for BEST
for BEST
