Normalized Mutual Information

Definition

• Based on Mutual Information, Normalized Mutual Information includes a normalization factor:

  where $S_X$ denotes the number of states of $X$.

• This means that the Mutual Information $I(X,Y)$ is divided by the maximum possible entropy of $X$, i.e., $\log _2({S_X})$.

• With that, the formal definition of Normalized Mutual Information is:

Usage

• BayesiaLab reports the Normalized Mutual Information in the Target Analysis Report: Menu > Analysis > Report > Target > Relationship with Target Node.
• Note that this table shows the Normalized Mutual Information of each node, e.g., XRay, Dyspnea, etc., with regard to the Target Node, Cancer.

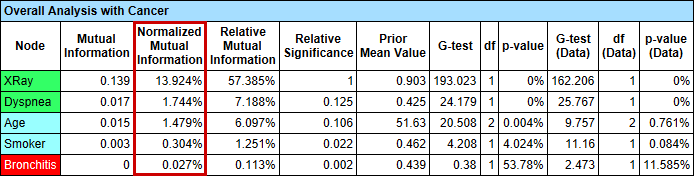
• The Normalized Mutual Information can also be shown by selecting Menu > Analysis > Visual > Overall > Arc > Mutual Information and then clicking the Show Arc Comments icon or selecting Menu > View > Show Arc Comments.

• Note that the corresponding options under Menu > Preferences > Analysis > Visual Analysis > Arc's Mutual Information Analysis have to be selected first:

  

• In Preferences, Child refers to the Normalized Mutual Information from the Parent onto the Child node, i.e., in the direction of the arc.

• Conversely, Parent refers to the Normalized Mutual Information from the Child onto the Parent node, i.e., in the opposite direction of the arc.