Target Mean Analysis

Context

• This analysis visualizes the relationships of selected Driver Nodes in a network with the Target Node in the form of curves.
• Performing this analysis is often used as a reference point in a key driver analysis see Chapter 8.

Example

• The following example is taken from Chapter 8: Chapter 8: Probabilistic Structural Equation Models for Key Driver Analysis
• The network below features a the Target Node at the center of the network for which we want to analyze its response to changes of the Driver Nodes connected to it.
  • The the node $Pleasure\_(4)$ is the Target Node.
  • The nodes $Pleasure$, $Corresponds$, $Easy\, to\, wear$, and $Intensity$ are the Driver Nodes under investigation.
  • In traditional statistics, the Target Node would be the dependent variable, and the Driver Nodes would be considered independent variables.
    

Usage

• Make sure you have defined a Target Node.
• In Validation Mode F5, select the of interest, i.e., the Driver Nodes, and go to Menu > Analysis > Visual > Target > Target's Posterior > Curves > Total Effects.
• If you have not selected any node, BayesiaLab will use all connected and observable nodes for the analysis.

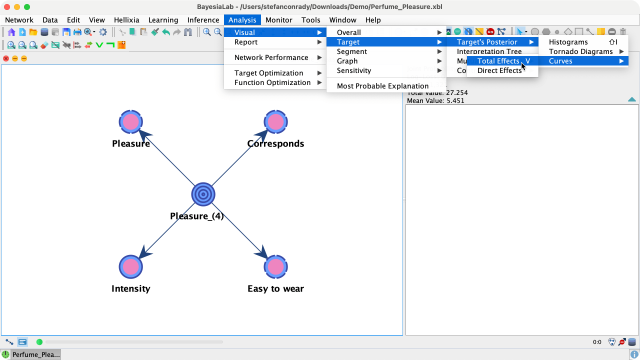
• A window comes up, which allows you to set several options for the chart to be displayed.

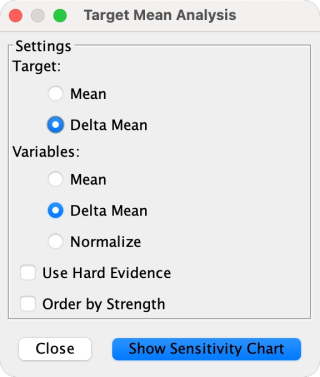
• Given that our Driver Nodes were not all recorded on the same scale, and for the ease of interpretation, we check the Delta Mean boxes for both Variables and Target.
• Clicking the Show Sensitivity Chart button brings up the plot.

• In this chart, we see two simulations:
  • The x-values of each Driver Node are simulated across their variation domain using Minimum Cross-Entropy (see Chapter 7, Numerical Evidence — MinXEnt).
  • These x-values are used as inputs for inferring — with the network — the y-values of the Target Node.
• The x-y values pairs of Driver Nodes and Target Node produce a set of response curves, i.e., the Total Effects Curves.
• They are shown simultaneously and can be distinguished by their randomly-assigned colors.

Calculating Means

• In our example, all Driver Nodes are discrete with integer values. As a result, calculating the mean value of the Driver Nodes' states is straightforward.
• In alternative cases, BayesiaLab will compute mean values as follows:
  • If a node is categorical, but has numerical values associated with its categorical states, the mean is computed from the associated values.
  • If a node is continuous, its mean value is computed from the states' intervals.
  • If none of the above applies, BayesiaLab uses a set of default values enumerating the states beginning with 0 for the first state.

Interpretation

• This visual analysis show how changes in the mean values of the selected Driver Nodes in a network are associated with changes of the mean value of the Target Node.
• To provide some intuition for the mean value simulations of the x-values and the inferred y-values, the following panels compare the marginal distributions of all nodes with their posterior distributions after simulating a one-unit increase (using MinXEnt) for $Corresponds$.

Marginal Distributions	Posterior Distributions
$Corresponds=5.672$	$Corresponds=6.762\,(+1)$
$Pleasure\_(4)=5.872$	$Pleasure\_(4)=6.648$

• Compare the marginal distributions of the Target Node and the Driver Nodes (on the left) with the posterior distributions of the same nodes on the right
• Here, the +1 increase in $Corresponds$ is associated with a 0.78 increase in the mean value of the Target Node $Pleasure\_(4)$.

Workflow Illustration

Context

• This report calculates the Total Effect of each selected node (or all nodes) in the network on the Target Node.
• Generating this report is often used as a reference point in a key driver analysis see Chapter 8.

Total Effect Definition

• The Total Effect of a node on a Target Node is the derivative of the Total Effects Curve, computed at the a priori mean of that node, i.e., Delta Mean=0.

where $X$ is the node of interest and $Y$ is the Target Node.

• The Total Effect represents the impact of a small change of the "mean" of a node on the "mean" of a Target Node.
• The Total Effect is the ratio of these two values.

Total Effect Curve

• The Total Effect Curve is plotted using BayesiaLab's Target Mean Value Analysis function.

• For illustration purposes, we borrow a plot produced by another BayesiaLab function, the Target Mean Analysis.

• Delta Mean=0 is marked with a black dashed vertical line; the derivative of $Intensity$ is highlighted with a cyan-colored dashed tangent.