Data Perturbation (9.0)

Context

Learning | Data Perturbation

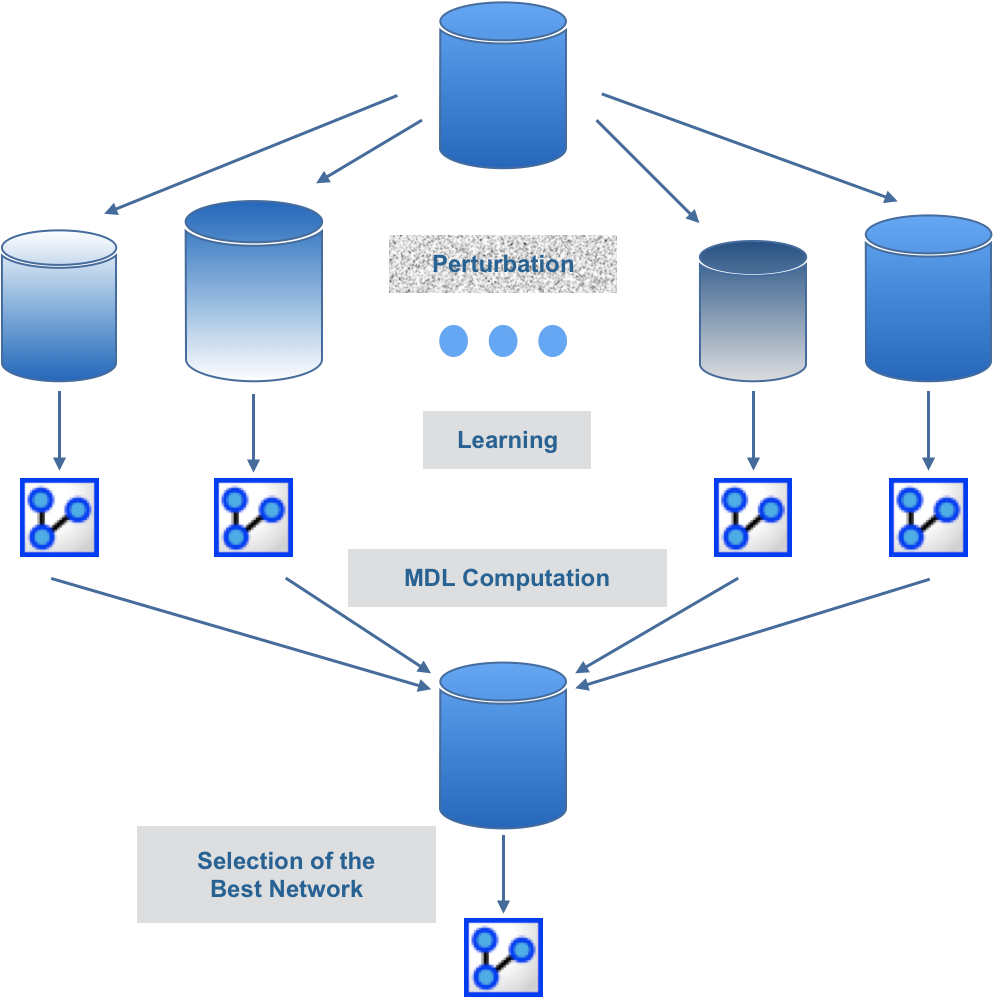
Data Perturbation (opens in a new tab) is a Smoothed Bootstrapping algorithm that randomly perturbs the weight of each particle described in the data set by multiplying the current weight by a random perturbation with values between 0 and 2. The perturbation value is drawn from a Normal distribution with a mean of 1 and a standard deviation set by the user. An internal decay factor can be used to progressively attenuate the standard deviation with each iteration in order to reach the user-defined Final Standard Deviation. When the Final Standard Deviation is set to 0, the last data set is therefore the original unperturbed data set.

The chosen learning algorithm is then run iteratively on each perturbed data set, and the MDL scores (opens in a new tab) of the induced networks are evaluated on the original unperturbed data set.

The network that is finally returned is the one with the lowest MDL score, estimated on the original unperturbed data set.

History

Data Perturbation (opens in a new tab) was previously updated in version 5.3 (opens in a new tab), 5.4 (opens in a new tab), and 6.0 (opens in a new tab).

New Feature: Structural Coefficient

As of version 9.0, the perturbation can be done locally at the particle level, but also globally, at the data set level, with the possibility to generate a random Structural Coefficient (opens in a new tab).

The Structural Coefficient allows modifying the number of particles that are perceived during structural learning. Choosing a value less than 1 is equivalent to increasing the number of particles and therefore the sensitivity of the learning algorithms. Choosing a value greater than 1 is equivalent to reducing the number of particles and thus makes the learning algorithms more conservative. This parameter basically represents a way of modifying the significance threshold to represent relationships with arcs.

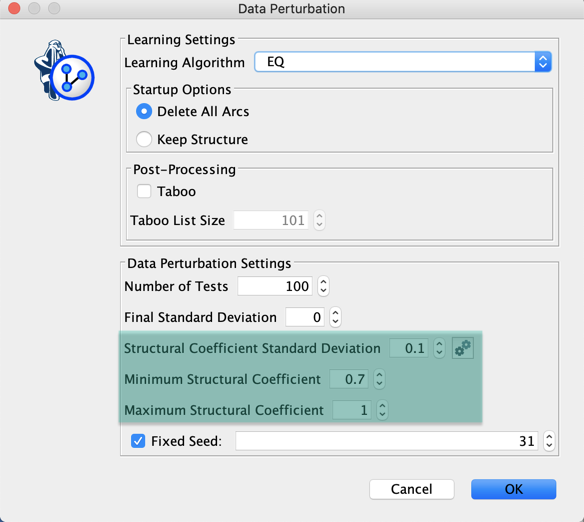
When the Structural Coefficient Standard Deviation is set to a value greater than 0, a random coefficient is drawn, for each perturbed data set, from a Normal distribution with a mean equal to the Default Structural Coefficient (the one associated with the current Bayesian network), and the specified standard deviation.

Clicking  allows getting the range of coefficients that can be drawn with the Default Structural Coefficient and Structural Coefficient Standard Deviation. It is then possible to edit the Minimum and Maximum Structural Coefficients. In the example above, we are using a truncated Normal distribution for not creating perturbed data sets with a Structural Coefficient greater than the Default Structural Coefficient.