Supervised Learning: Structural Coefficient Analysis
Up to this point, the differences in model structure and the corresponding performance were a result of the learning algorithm, i.e., Markov Blanket vs. Augmented Markov Blanket.
Now we explore how different levels of network complexity could potentially improve the Augmented Markov Blanket model. In other words, could a more complex network provide better performance without risking over-fitting?
Structural Coefficient
To modify a network’s complexity, we now introduce the Structural Coefficient .
Throughout this chapter, we abbreviate “Structural Coefficient ” with “SC.”
This parameter allows changing the internal number of observations and, thus, determines a kind of “significance threshold” for network learning. Consequently, it influences the degree of complexity of the induced networks. The internal number of observations is defined as:
where is the number of samples in the dataset.
By default, SC is set to 1, which reliably prevents the learning algorithms from overfitting the model to the data. However, in studies with relatively few observations, the analyst’s judgment is needed regarding whether a downward adjustment of this parameter can be justified. Reducing SC means increasing , which is like increasing the number of observations in the dataset via resampling.
On the other hand, increasing SC beyond 1 means reducing , which can help manage the complexity of networks learned from large datasets. Conceptually, reducing is equivalent to sampling the dataset.
Structural Coefficient Analysis
We now perform a Structural Coefficient Analysis on the basis of the Augmented Markov Blanket, which generates several metrics that help to trade off between complexity and fit: Menu > Tools > Multi-Run > Structural Coefficient Analysis.
Note that we use the original Learning/Test Set split again, which allows us to directly compare the in-sample and out-of-sample predictive performance as a function of varying SC levels.
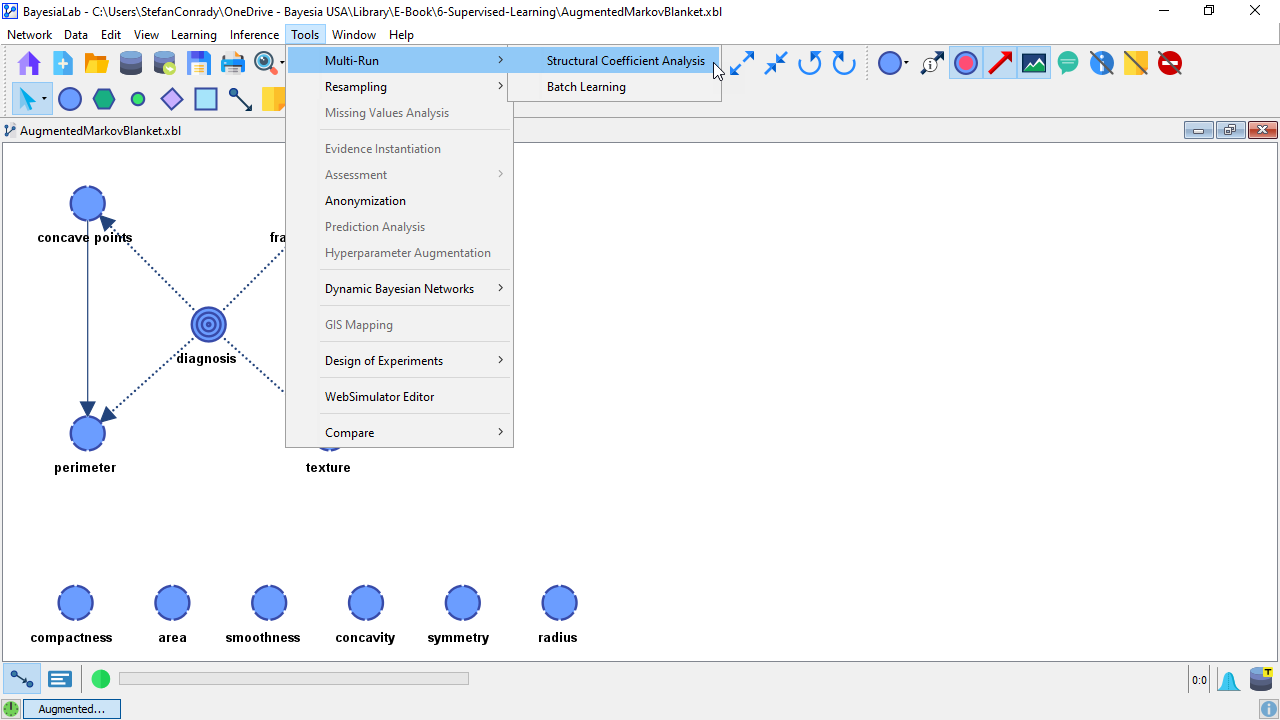
BayesiaLab prompts us to specify the range of SC values to be examined and the number of iterations to be performed. It is worth noting that the minimum SC value should not be set to 0, or even close to 0, without careful consideration.
An SC value of 0 would create a fully connected network, which can take a very long time to learn, depending on the number of variables, or even exceed the memory capacity of the computer running BayesiaLab. Technically, SC=0 implies an infinite dataset, which results in all relationships between nodes becoming significant.
Setting the Number of Iterations determines the interval steps to be taken within the specified range of the Structural Coefficient. We choose 10 iterations over an SC range between 0.1 and 1, which gives us increments of 0.1. With more complex models and more data, we might be more conservative and start with a narrower range, e.g., 0.5 to 1.
Clicking OK opens up a report that shows the range of changes due to modifying the Structural Coefficient.
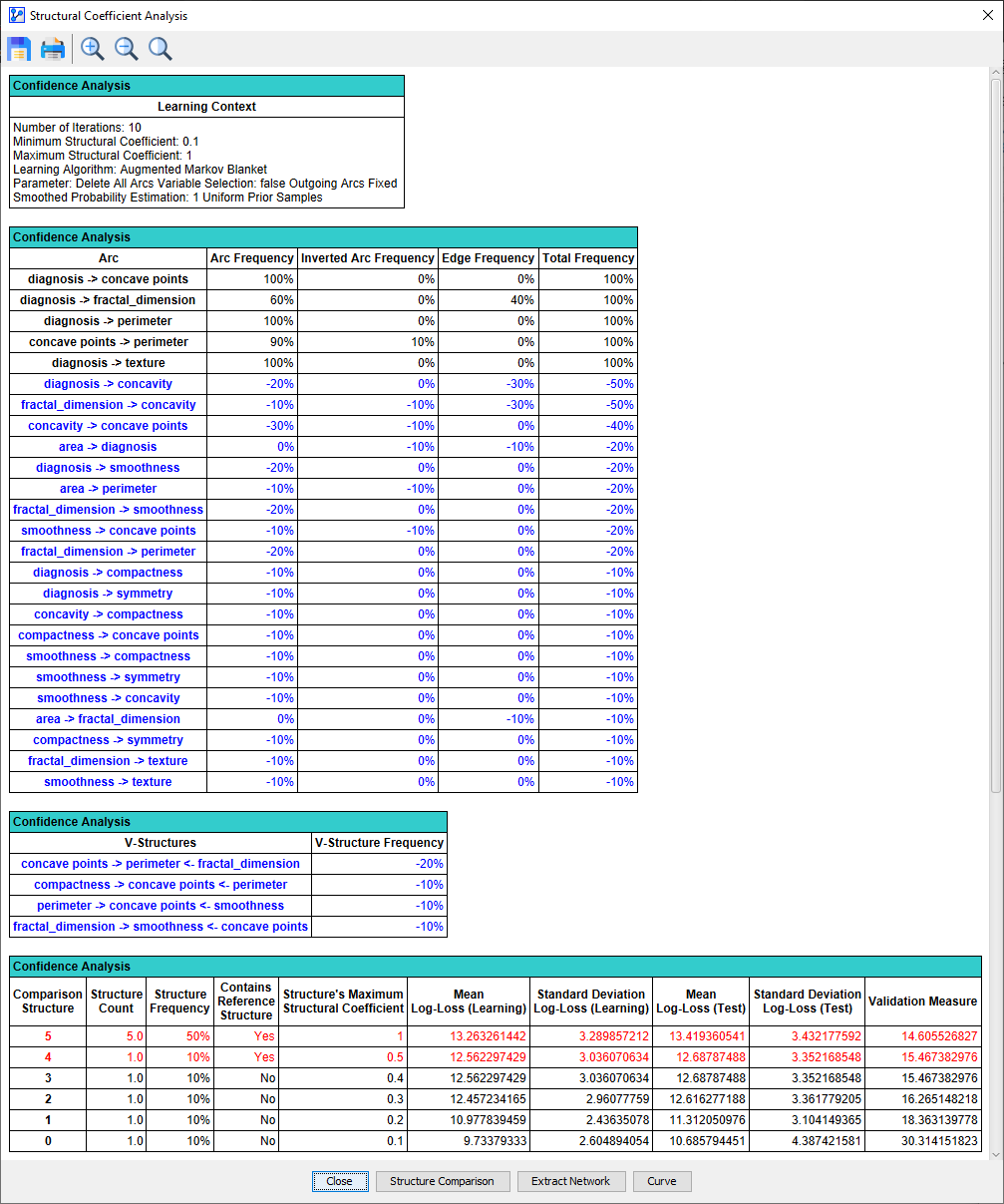
We only show a portion of the report here and omit a discussion of its elements. For a thorough explanation of this report, please see Structural Coefficient Analysis.
Instead, we focus on the Curve function, which can be activated by clicking on the corresponding button at the bottom of the report. This tool can plot the metrics that we specified earlier in the settings as we started the Structural Coefficient Analysis.
Our objective is to determine the correct level of network complexity for reliably high predictive performance while avoiding the over-fitting of the data. By clicking Curve, we can plot several different metrics for this purpose.
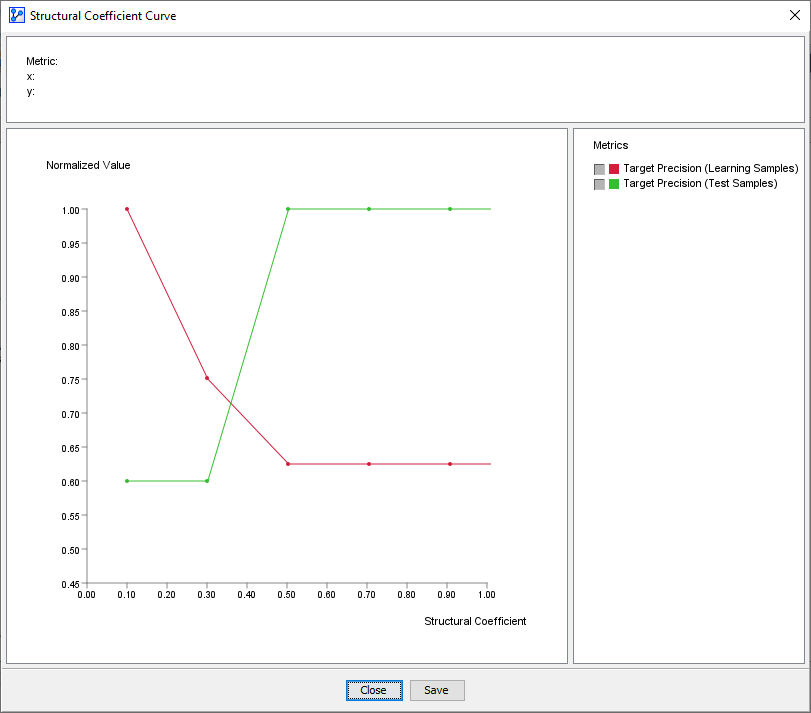
Structure/Target Precision Ratio
Selecting Structure/Target Precision Ratio provides a helpful measure for making trade-offs between predictive performance versus network complexity.
This plot can be best interpreted when following the curve from right to left. Moving to the left along the x-axis lowers the Structural Coefficient, which, in turn, results in a more complex Structure.
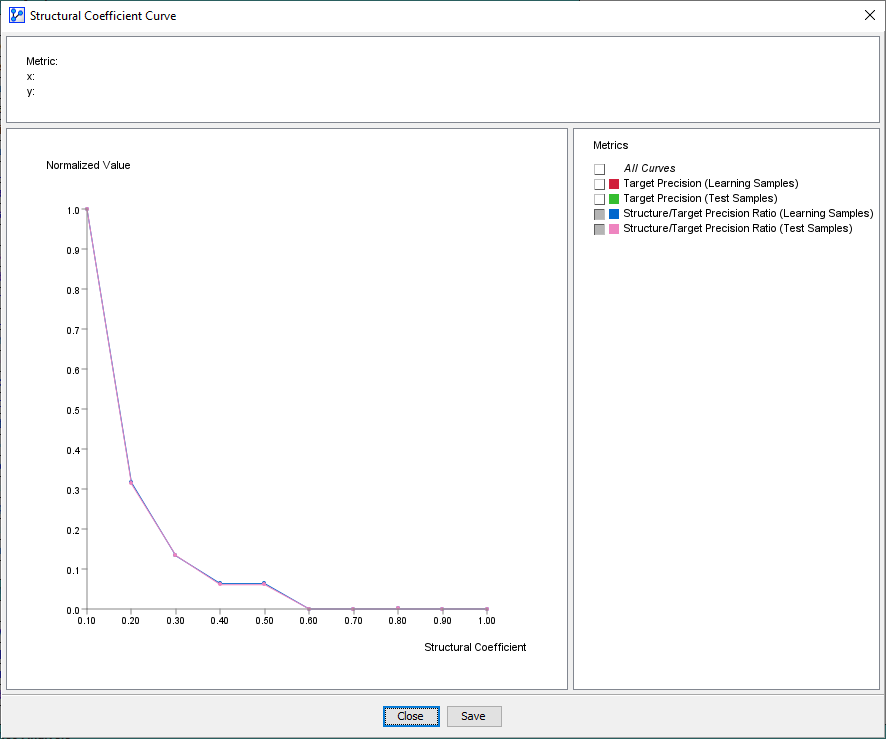
It becomes problematic when the Structure value increases faster than the Precision value, i.e. we increase complexity without improving Precision.
Typically, the “elbow” of the L-shaped curve identifies this critical point. Here, a visual inspection suggests that the “elbow” is around SC=0.4. The portion of the curve further to the left on the x-axis, i.e., SC <0.4, shows that the structure is increasing without improving precision, which suggests overfitting. Hence, SC=0.4 could be a good value to examine further.
Another sign of overfitting is when the predictive performance of a model starts to diverge between the Learning Set and the Test Set. This means that the out-of-sample performance is no longer comparable to the in-sample performance.
This is precisely what we can observe with the Target Precision Curves for both the Learning Set and the Test Set. For SC>0.5, the curves are parallel, which means that in-sample and out-of-sample performance move in sync. However, as the SC value drops below 0.5, the Learning Set performance increases while the Test Set performance drops, i.e., the curves diverge. The Target Precision for the Learning Set keeps increasing, while the Target Precision for the Test Set drops.
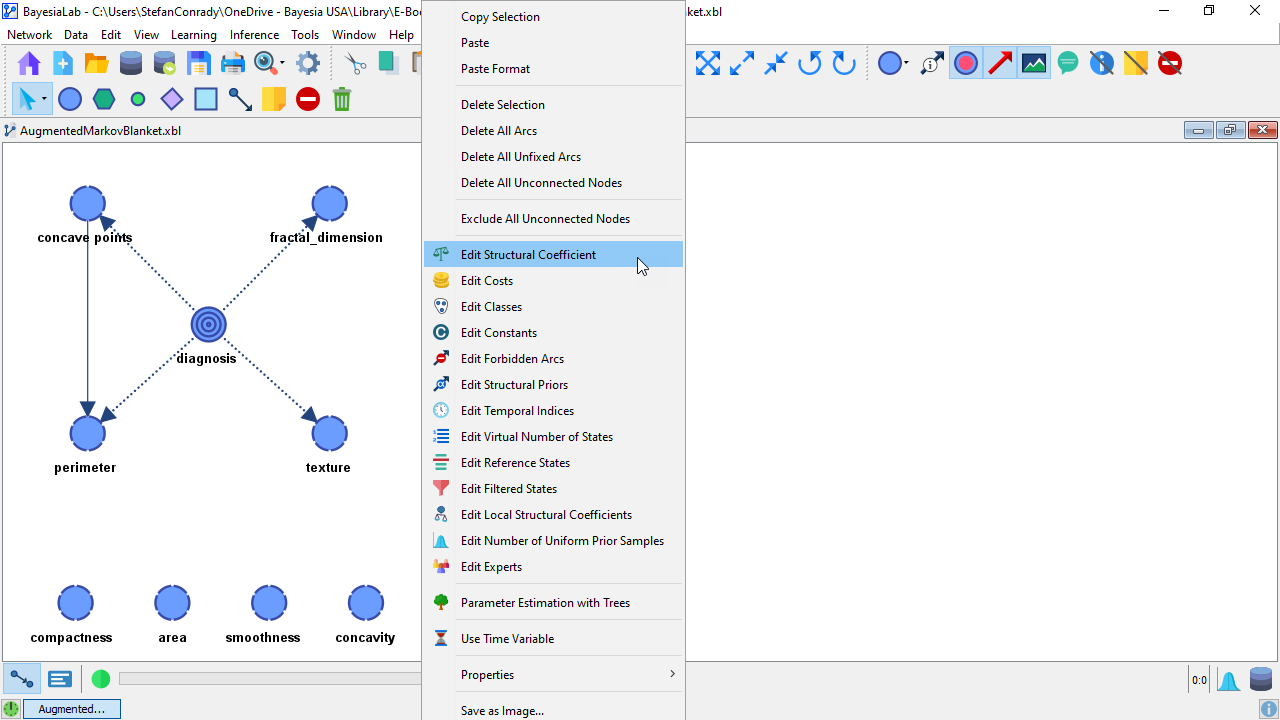
Augmented Markov Blanket (SC=0.5)
Having considered the curves in both of the above plots, we choose SC=0.5 for further evaluation.
The SC value can be set by right-clicking on the background of the Graph Panel and then selecting Edit Structural Coefficient from the Node Context Menu or via the menu: Menu > Edit > Edit Structural Coefficient.
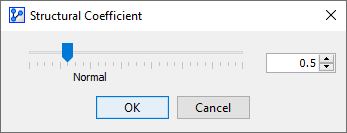
The SC value can then be set with a slider or by typing in a numerical value.
The Structural Coefficient icon now indicates that we are employing an SC value other than the default of 1.
The Structural Coefficient icon features an unbalanced scale. This symbolizes that we departed from the balanced weighting of fit and complexity. Instead, we have “put our thumb on the scale” to pursue a better fit of our model while accepting a higher complexity.
After returning to the Modeling Mode F4 we relearn the network using the same Augmented Markov Blanket algorithm as before.
As expected, this produces a more complex network.
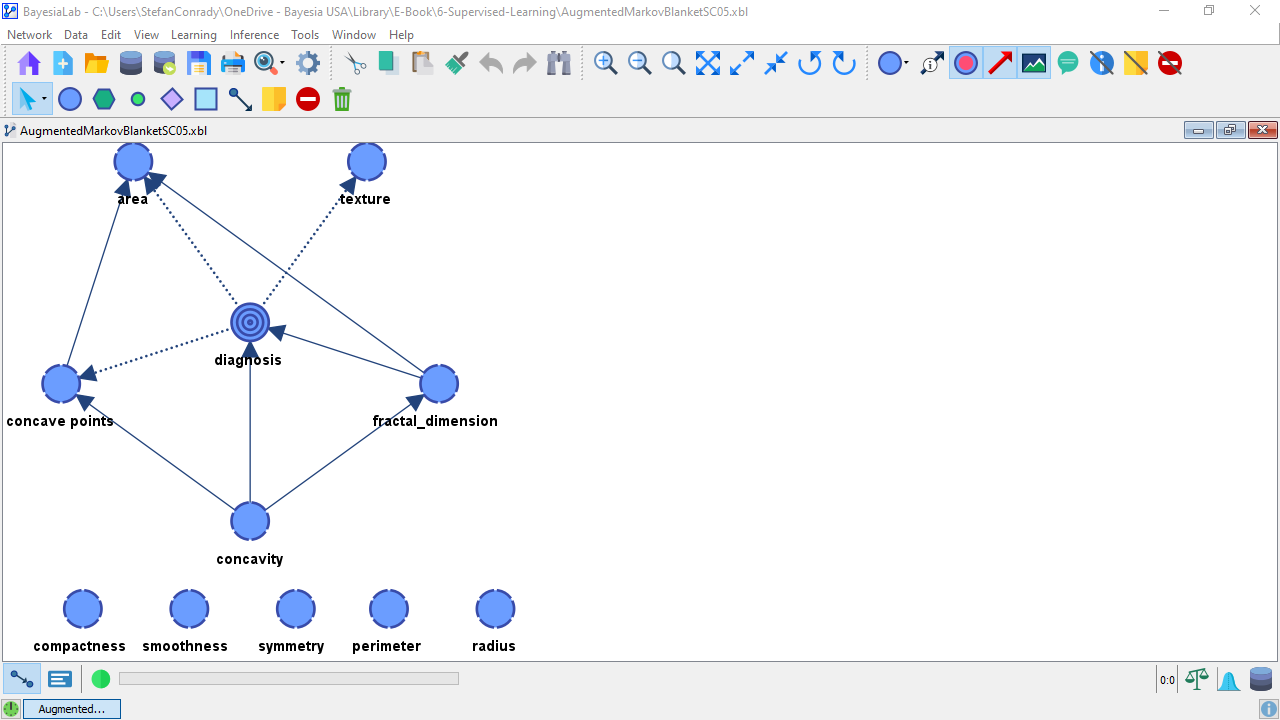
The key question is, will this increase in complexity deliver a performance advantage over the previously learned models?
Performance Analysis
So, we perform K-Folds Cross-Validation again, this time using the Augmented Markov Blanket at SC=0.5. The right panel in the overview below shows the results.
For comparison, we also show the performance of the earlier models we learned, i.e., the Markov Blanket (SC=1) in the left panel and the Augmented Markov Blanket (SC=1) in the center panel.
Among a myriad of other available measures, we have typically referenced the Overall Precision for evaluation purposes. In this regard, the latest Augmented Markov Blanket (SC=0.5) does not show an improvement, i.e., the Overall Precision remains at 94.2%
So, is there any benefit to the added complexity? It would depend on the context. Here, the objective is to distinguish between benign and malignant cell samples. Presumably, a false negative would be the worst forecast error. It would label a malignant sample as benign and perhaps cause a delay in a patient’s treatment.
Focusing on the False Negative Rate of the three models, we see an improvement from 11.32% (left) to 9.43% (center) to 8.49% (right). This means that the best model in this regard reduces the number of False Negatives by one-third.
There are numerous other approaches available in BayesiaLab to help improve the model further, e.g., choosing a different learning algorithm, learning structural priors, reviewing the discretization, etc.
However, for the purposes of this tutorial, we conclude our model optimization efforts here and continue on the basis of the Augmented Markov Blanket (SC=0.5) in the next section: Model Inference.
