Most Relevant Explanations (9.0)

Context

Analysis | Report | Evidence | Most Relevant Explanations

This new feature uses a genetic algorithm for searching partial instantiations of sets of variables that maximize the Generalized Bayes Factor (GBF) as the best explanations for a given set of evidence.

It is mainly based on the article written by Yuan, C. et al. (2011), "Most Relevant Explanations in Bayesian Networks (opens in a new tab)", Journal of Artiﬁcial Intelligence Research, pp. 309-352.

The Weight of Evidence (WoE), the logarithm of the GBF, dates back to work by Alan Turing in World War II (see Good, I. J. (1985), "Weight of Evidence: A Brief Survey (opens in a new tab)", Bayesian Statistics 2, pp. 249-270, for more general discussion of history and concepts):

where

E represents the current set of evidence (any type of evidence on any number of variables) for which we are seeking concise and precise explanations, and
H is the hypothesis described with hard evidence on a subset of variables

where is the negation of H, and O(.) denotes the odds:

As we can see, the GBF is expressed with two equivalent terms:

, a likelihood ratio,
, an odds ratio.

Even though they are strictly equivalent, the likelihood ratio is a natural interpretation of the GBF when the explanation H you are looking for belongs to the Ancestors of E in your Causal Bayesian Network (i.e. you assume that all arcs are in the causal direction and do not represent mere associations). On the other hand, you can interpret the GBF as an odds ratio either when your network is not causal, or when the explanation H you are looking for does not belong exclusively to the Ancestors of E.

The following wizard will help you set the options you want to use for searching the most relevant explanations of your current set of evidence E.

It consists of 4 main sections.

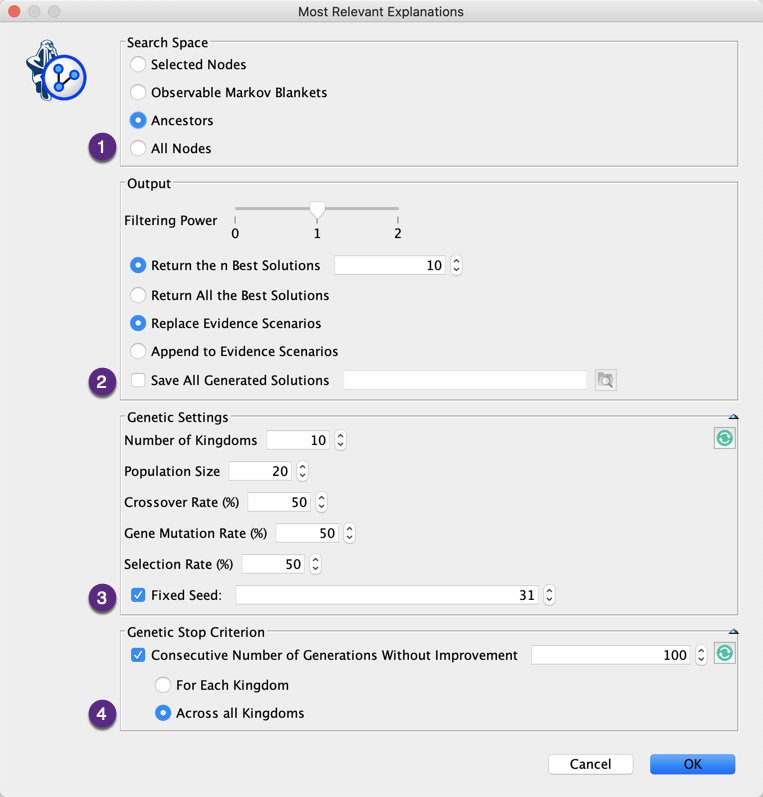
1. Search Space

This defines which nodes will be included in the search. The nodes that belong to E and those that are Not Observable (opens in a new tab) are excluded from the search. There are 4 options:

The Selected Nodes,
The nodes that belong to the Observable Markov Blanket(s) of the E,
The Ancestors of E,
All Nodes.

The choice of the Ancestors option only makes sense when your network is causal.

2. Output

There are different available options for setting the output (Report and Evidence Scenario File):

Filtering Power:
- 0: All solutions are reported,
- 1: The Strongly Dominated solutions are excluded from the report. Hs is strongly dominated by Hd, a dominant explanation when Hs ⊃ Hd and GBF(Hd) ≥ GBF(Hs),
- 2: The Strongly and Weakly Dominated solutions are excluded from the report. Hw is weakly dominated by Hd, when Hw ⊂ Hd and GBF(Hd) > GBF(Hw),
Return the n Best Solutions: returns only a subset of (filtered) solutions,
Return All the Best Solutions: returns all (filtered) solutions,
Replace Evidence Scenarios: replaces your current scenarios with the returned explanations,
Append to Evidence Scenarios: adds the return explanations to your current evidence scenarios,
Save All Generated Solutions: saves all (unfiltered) explanations in a file.

3. Genetic Settings

The BayesiaLab's MRE feature is using our genetic algorithm for searching the best explanations. This genetic algorithm can be customized:

Number of Kingdoms: number of populations that evolve independently,
Population Size: number of individuals/solutions per population,
Crossover Rate: the probability for the individuals of the worst kingdom to be generated by crossing the genes of the best individuals of two randomly selected kingdoms,
Gene Mutation Rate: the probability to mute a gene of an individual,
Selection Rate: the probability for an individual to be selected to breed the new generation,
Fixed Seed: this algorithm being stochastic, using a fixed seed allows you to reproduce your results.

Clicking allows you to go back to the default settings.

The iconsin the upper right corner allows you to show and hide these options respectively.

4. Genetic Stop Criterion

The genetic algorithm is an anytime algorithm that can run forever. If you do not want to stop it manually by clicking in the lower-left corner of the graph window, you can define a stop criterion based on the consecutive number of generations without any improvement. The number of generations without improvement can be calculated at the kingdom level or across all kingdoms.

Clicking allows you to go back to the default settings.

The iconsin the upper right corner allow you to show and hide these options respectively.

Example

Let's use the Causal Bayesian Network described in Yuan, C. et al. (2011), and originally defined in Poole, D., & Provan, G. M. (1991). What is the most likely diagnosis?. In Bonissone, P., Henrion, M., Kanal, L., & Lemmer, J. (Eds.), Uncertainty in Artiﬁcial Intelligence 6, pp. 89–105. Elsevier Science Publishing Company, Inc., New York, N. Y.

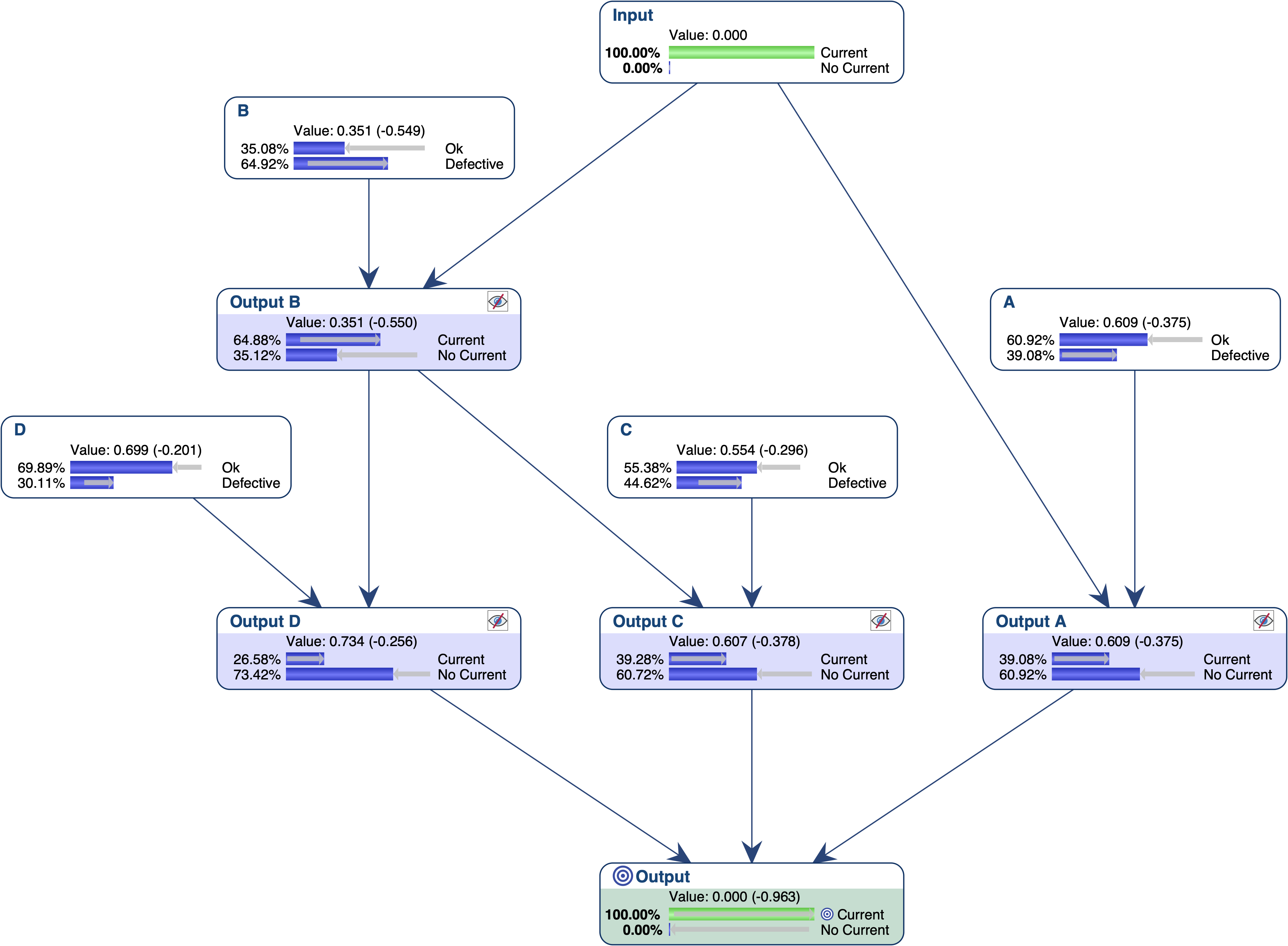
It models the following electric circuit, where gates A, B, C and D are Defective when they are closed. This means that there is a failure when Output = Current.

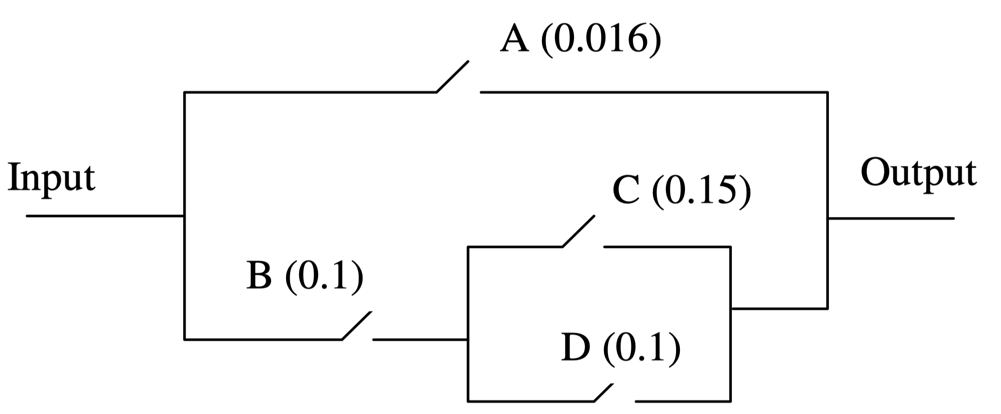
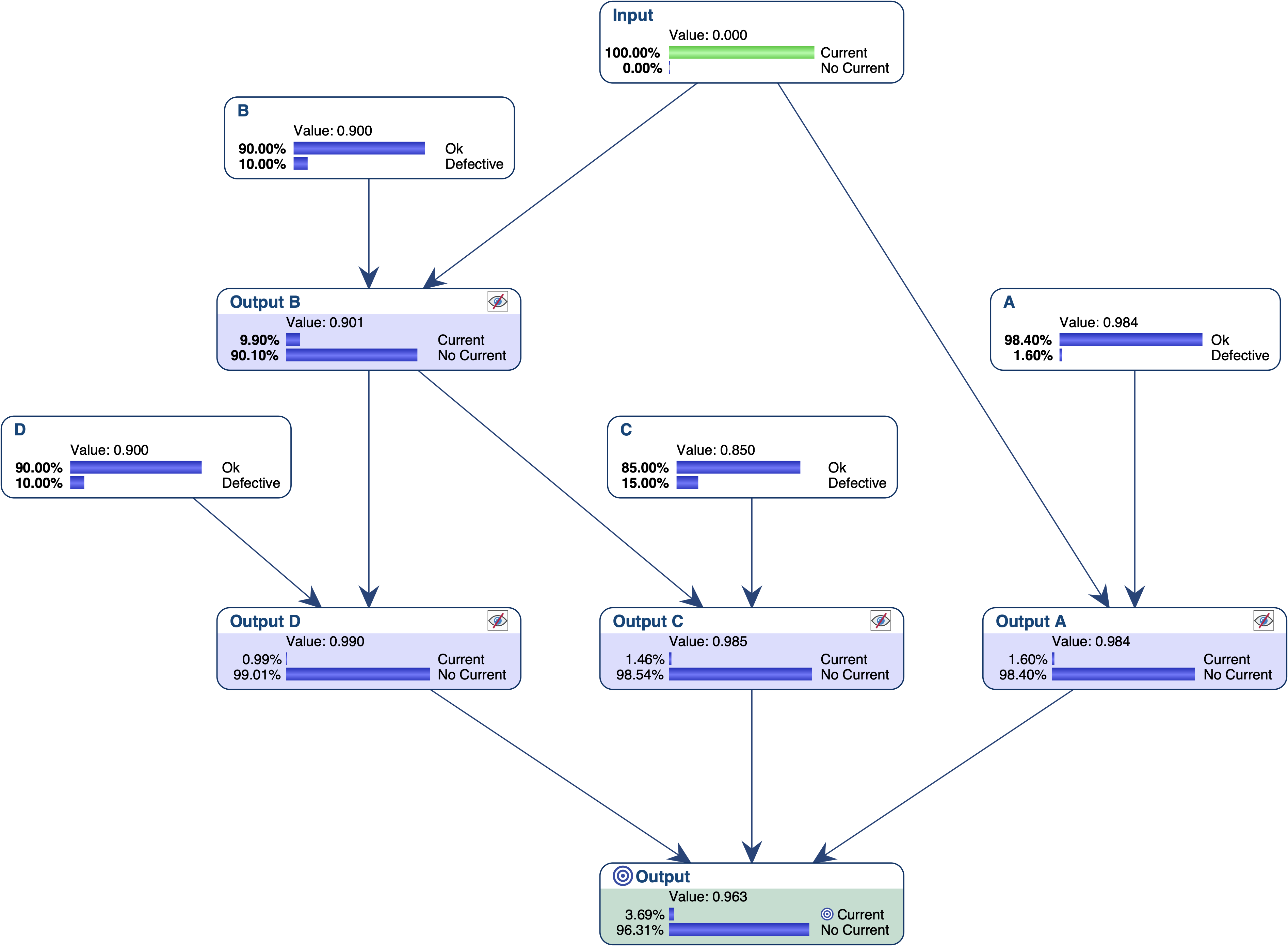
Let's suppose we want to find out what are the most relevant explanations for the failure of this system. Given that we want to find explanations in terms of gates, we first set the nodes that represent the local outputs as Not Observable (opens in a new tab), and then set Output = Current.

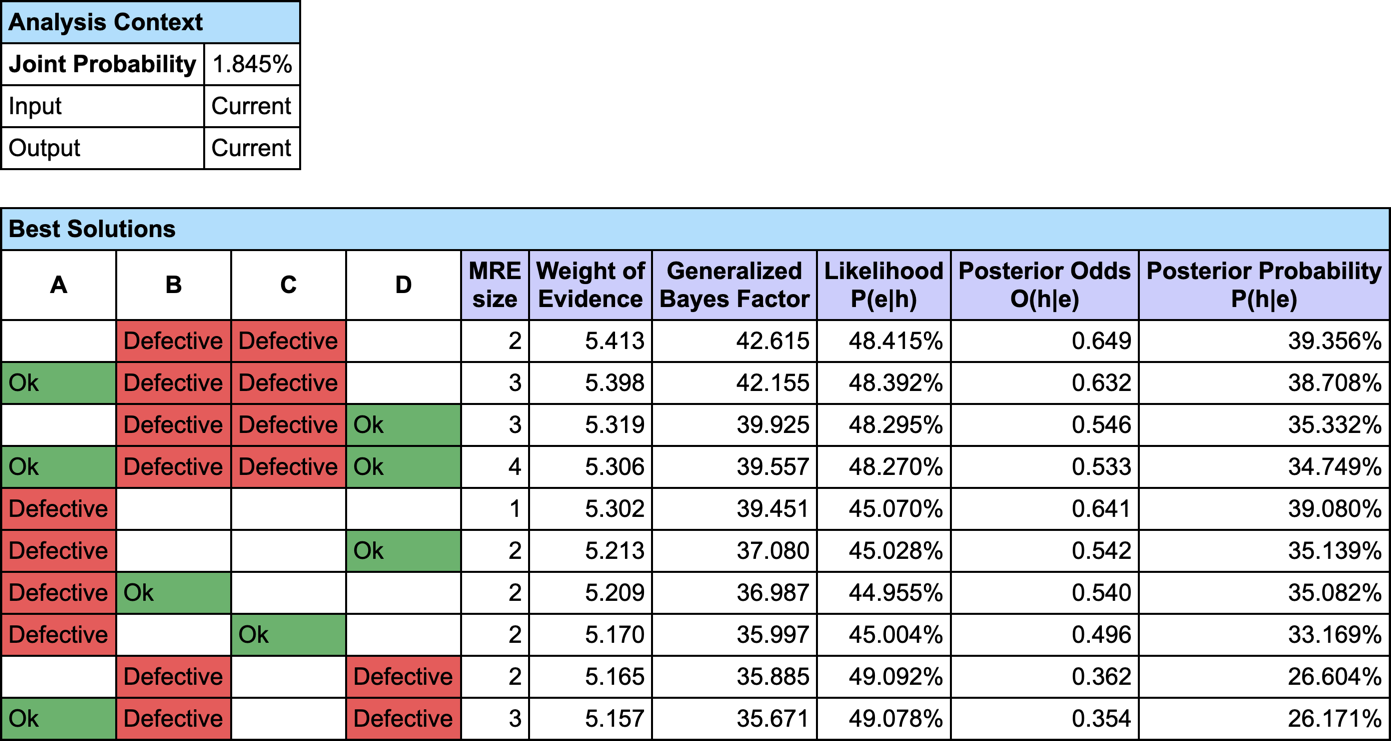
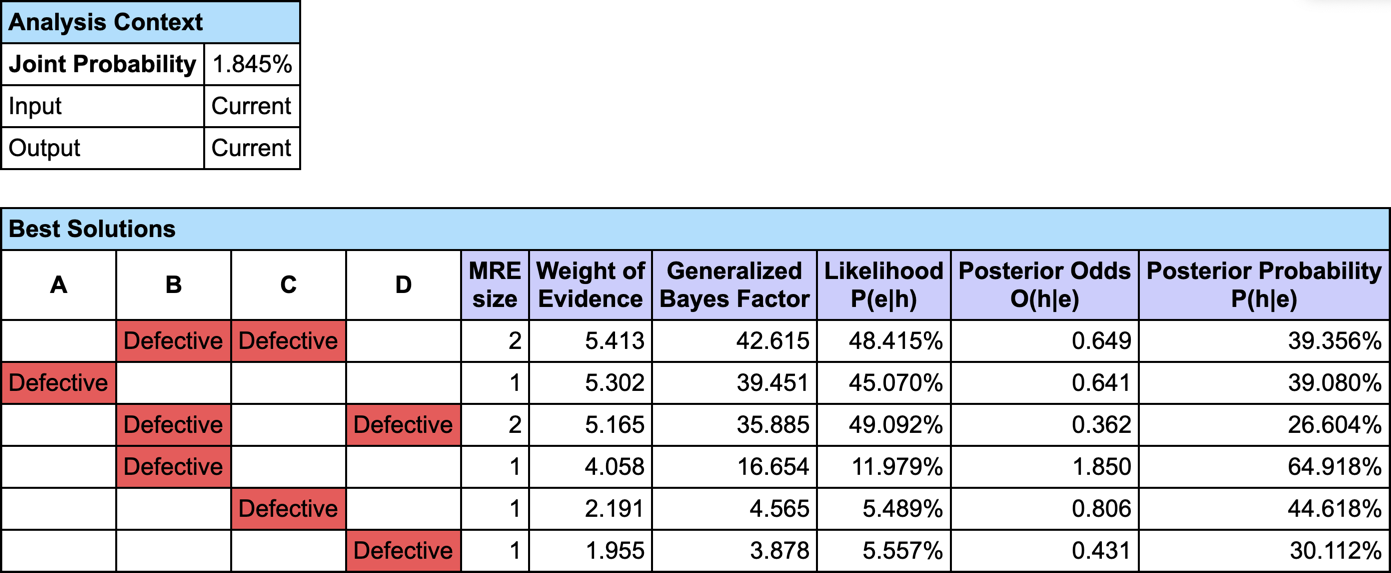
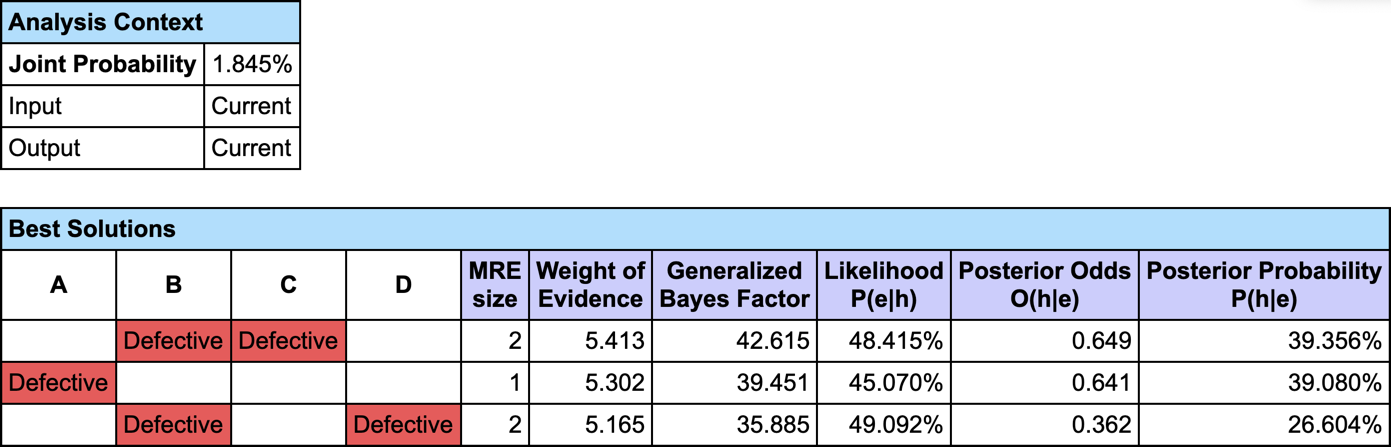
The most relevant explanation H* for the evidence is to have B and C Defective.

In addition to the description of the explanation, the generated report contains 6 measures:

MRE Size: the number of observations in *H. H** is made of 2 pieces of evidence, on B and C
Weight of Evidence: the binary logarithm of the Generalized Bayes Factor
Generalized Bayes Factor
Likelihood P(E|H)
Posterior Odds O(H|E)
Posterior Probability P(H|E)

Since our model is causal, we can use the likelihood ratio for interpreting the GBF. The likelihood that "B and C are Defective" is the cause of E is 42 times greater than the likelihood that "B or C are Ok" is the cause of E (48.4% versus 1.1%).

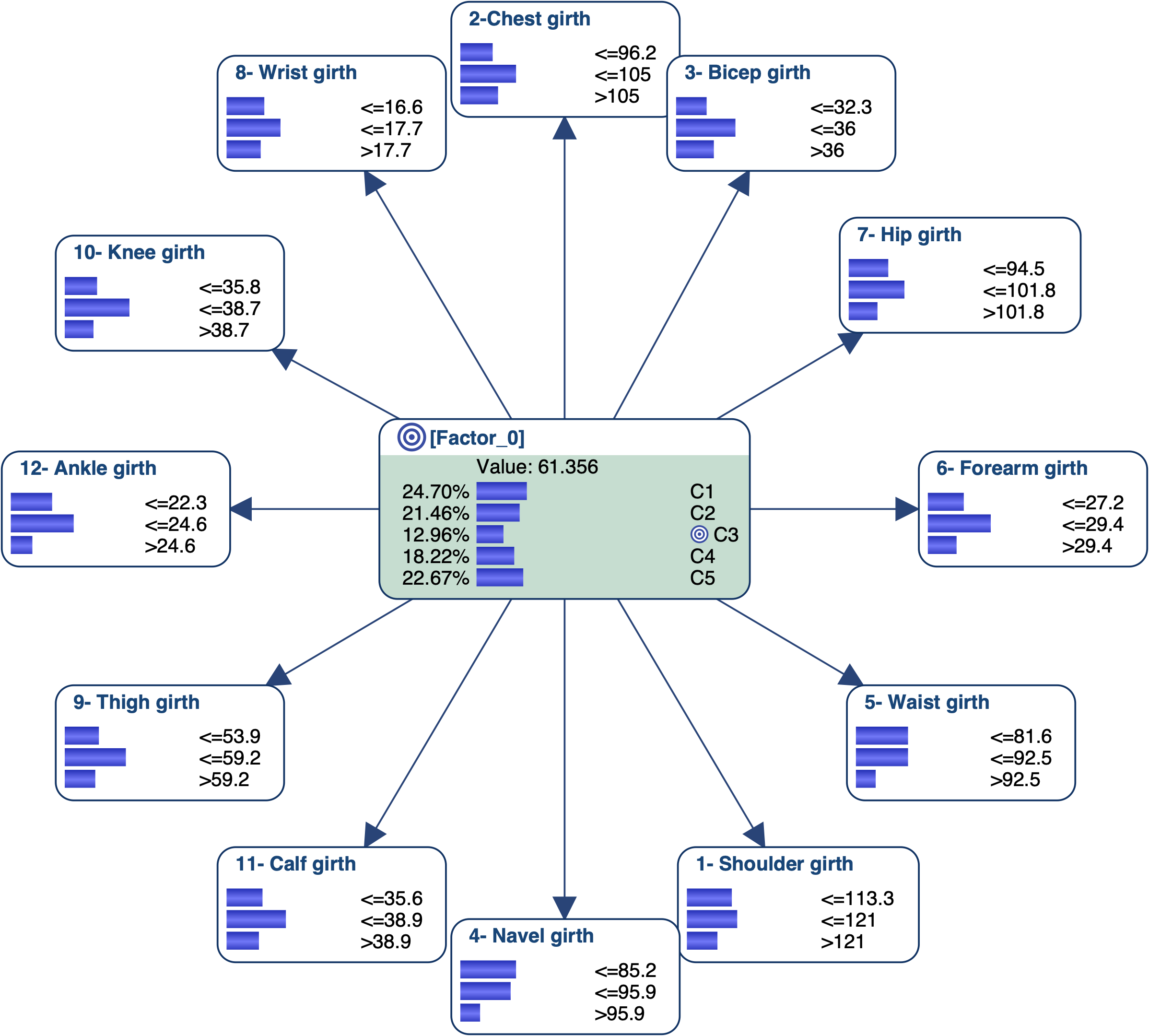
Let's suppose we have a data set that describes physically active men (several hours of exercise a week) with body girth measurements and skeletal diameter measurements. We used Data Clustering (opens in a new tab) in order to automatically create a latent variable that represents a typology of these men and found 5 clusters.

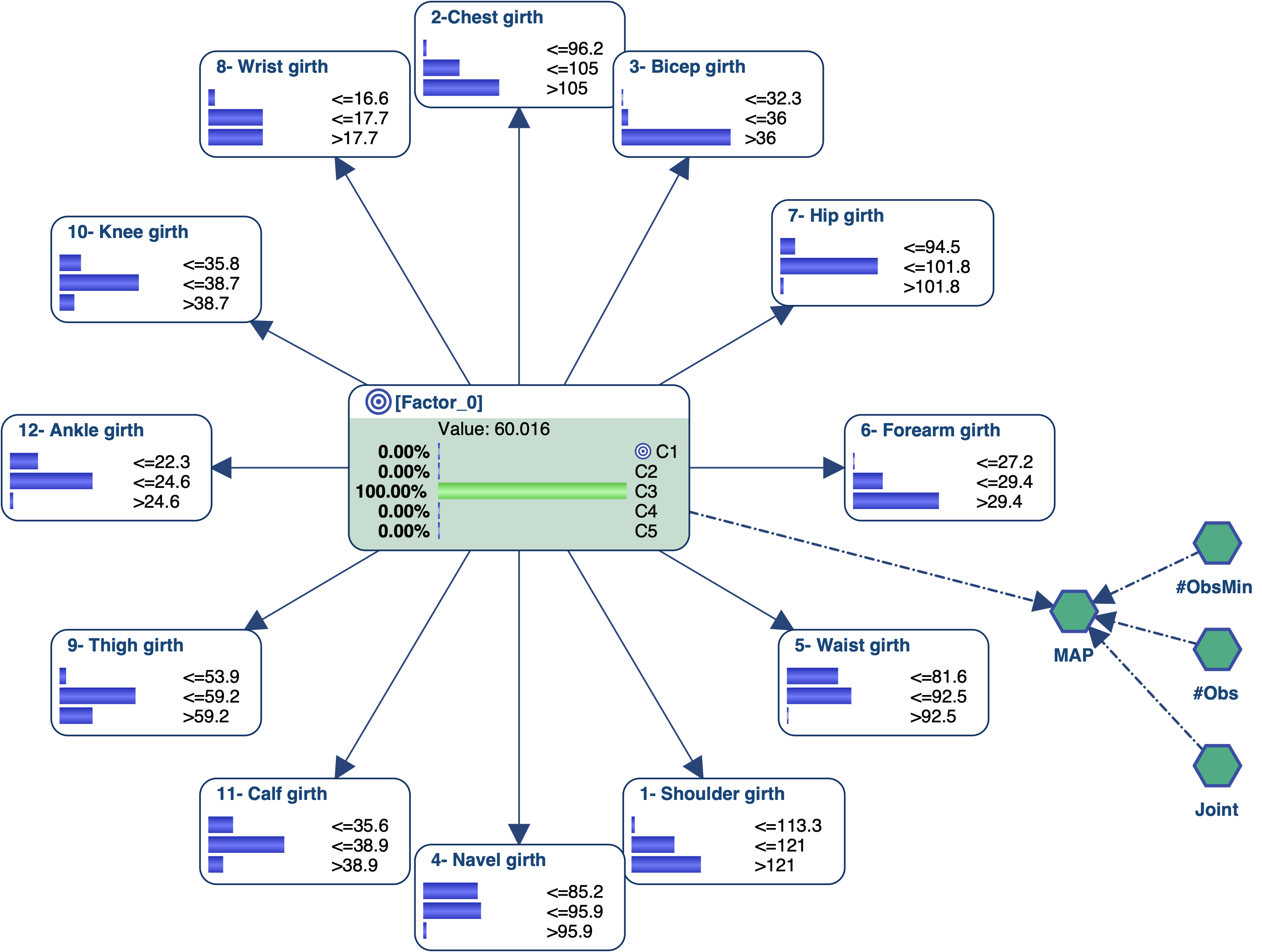
We know need to interact with the Bayesian network to try to associate an image/name with each state of the latent variable. We can obviously use the monitors and manually set evidence on each state of [Factor_0] to analyze the posterior probability distributions of all measurements. We can also use some tools that will automatically set evidence on the target node [Factor_0] or on the measurements.

Let's try to get the profile of the men that are associated with C3 and represent 13% of the overall population. We set C3 as the Target State.

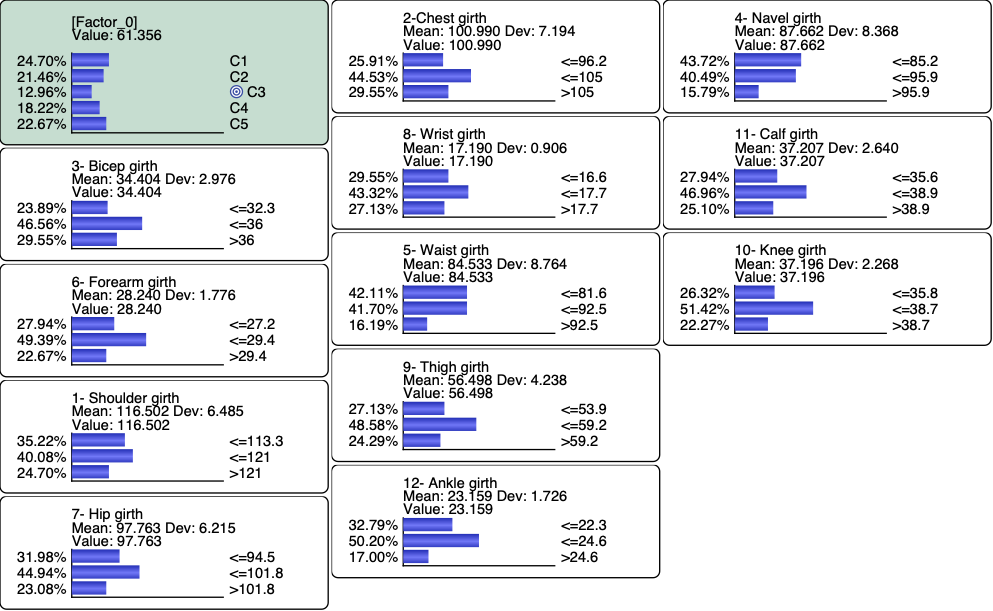
We can sort the monitors with respect to their correlation with C3 (Monitor | Sort | Target State Correlation, or via the Monitor Pane Contextual menu)

and then set a Hard Evidence on C3

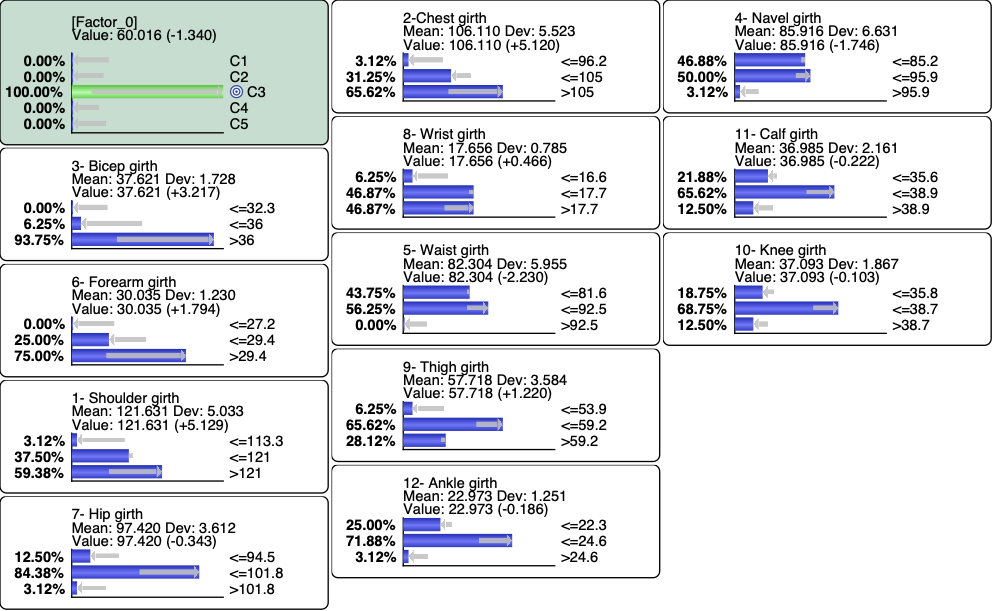
We can also use the Monitor Contextual menu to highlight the variations.

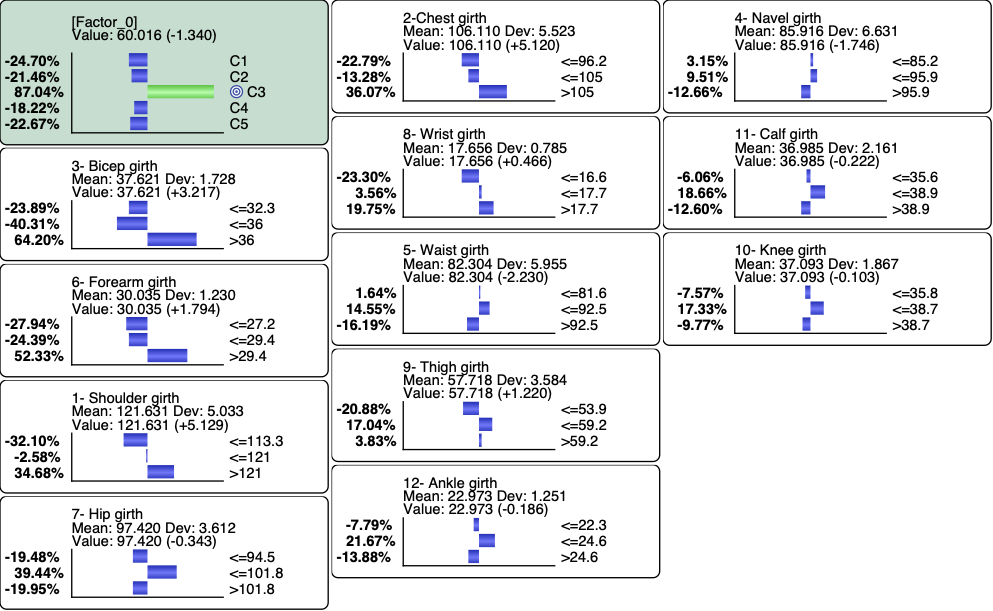
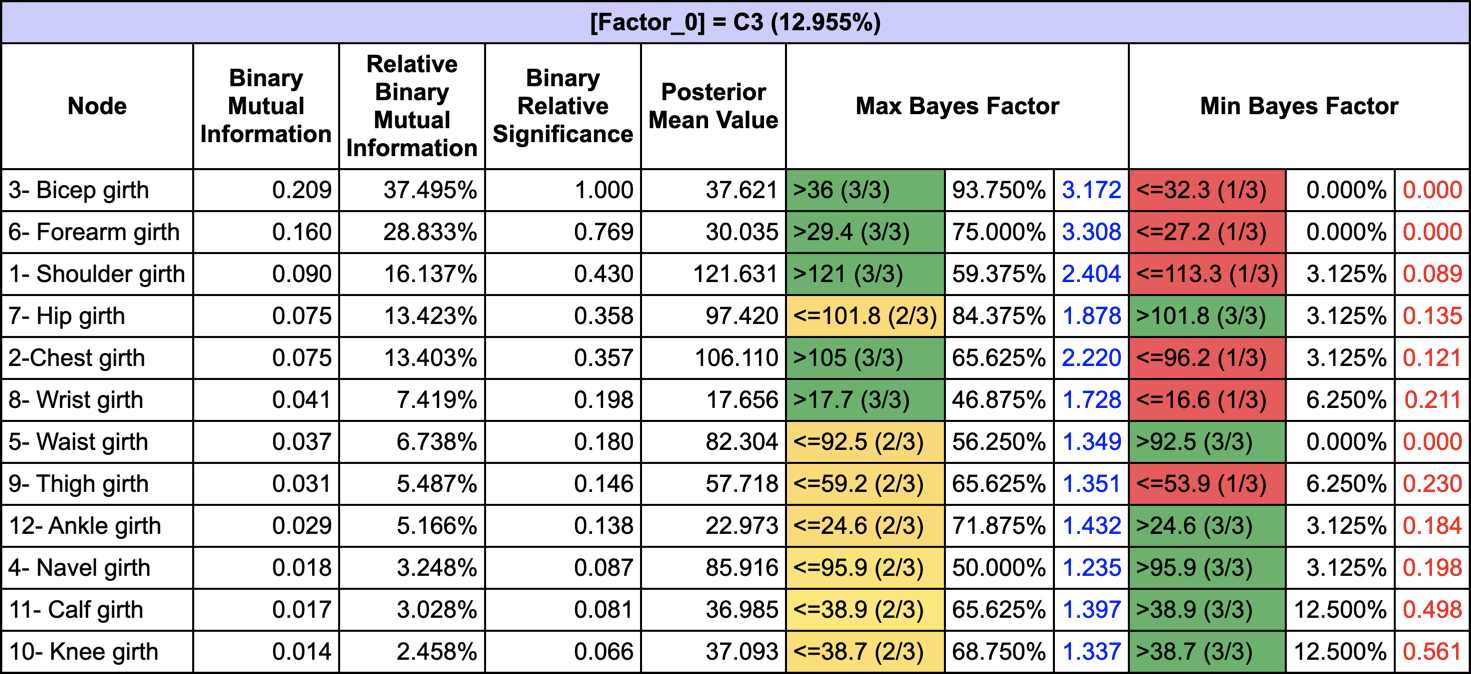
The Relationship with Target Node (Analysis | Report | Target | Relationship with Target Node) allows us to get all the posterior probabilities given C3 along with the Maximum and Minimum Bayes Factors:

The Mosaic Analysis (opens in a new tab) (Analysis | Visual | Overall | Mosaic) returns a graph with the posterior probability distributions of all measurements given each cluster:

The posterior distributions that correspond to C3 are represented in the third row of each block.

Since the measurements are numerical, we can analyze their Posterior Mean Values given each cluster (Report | Target | Posterior Mean Analysis (opens in a new tab)):

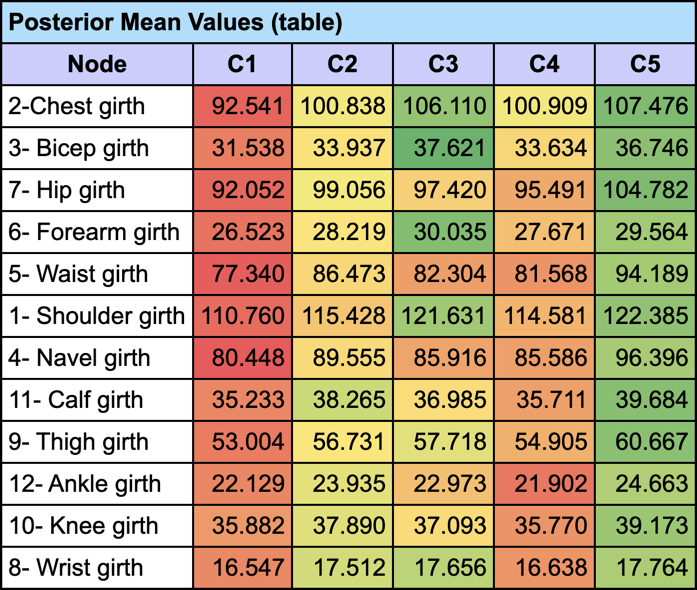
and generate the corresponding Radar Chart to visually compare the mean values given C3 with the prior values (i.e. on the entire population).

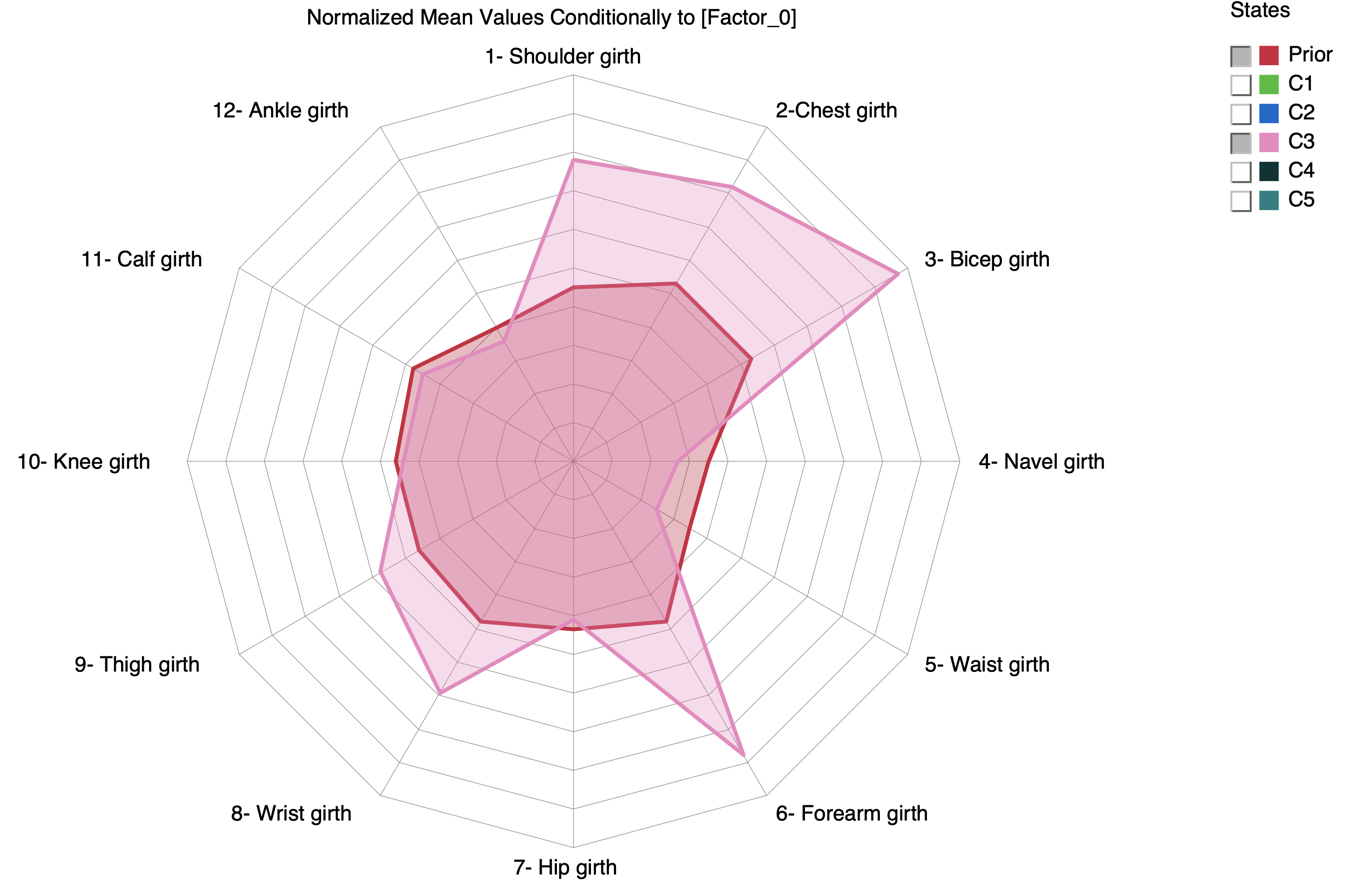
Note that we can get a similar Radar by using the Segment Profile Analysis (opens in a new tab) that we introduced in version 8.0 (Analysis | Visual | Segment | Profile):

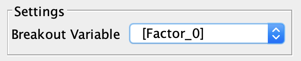
A square is added next to the label when the mean values of the Overall population and C3 are estimated as significantly different

for t-test (Frequentist)
for BEST (Bayesian)
Histograms
Tornado
Mosaic

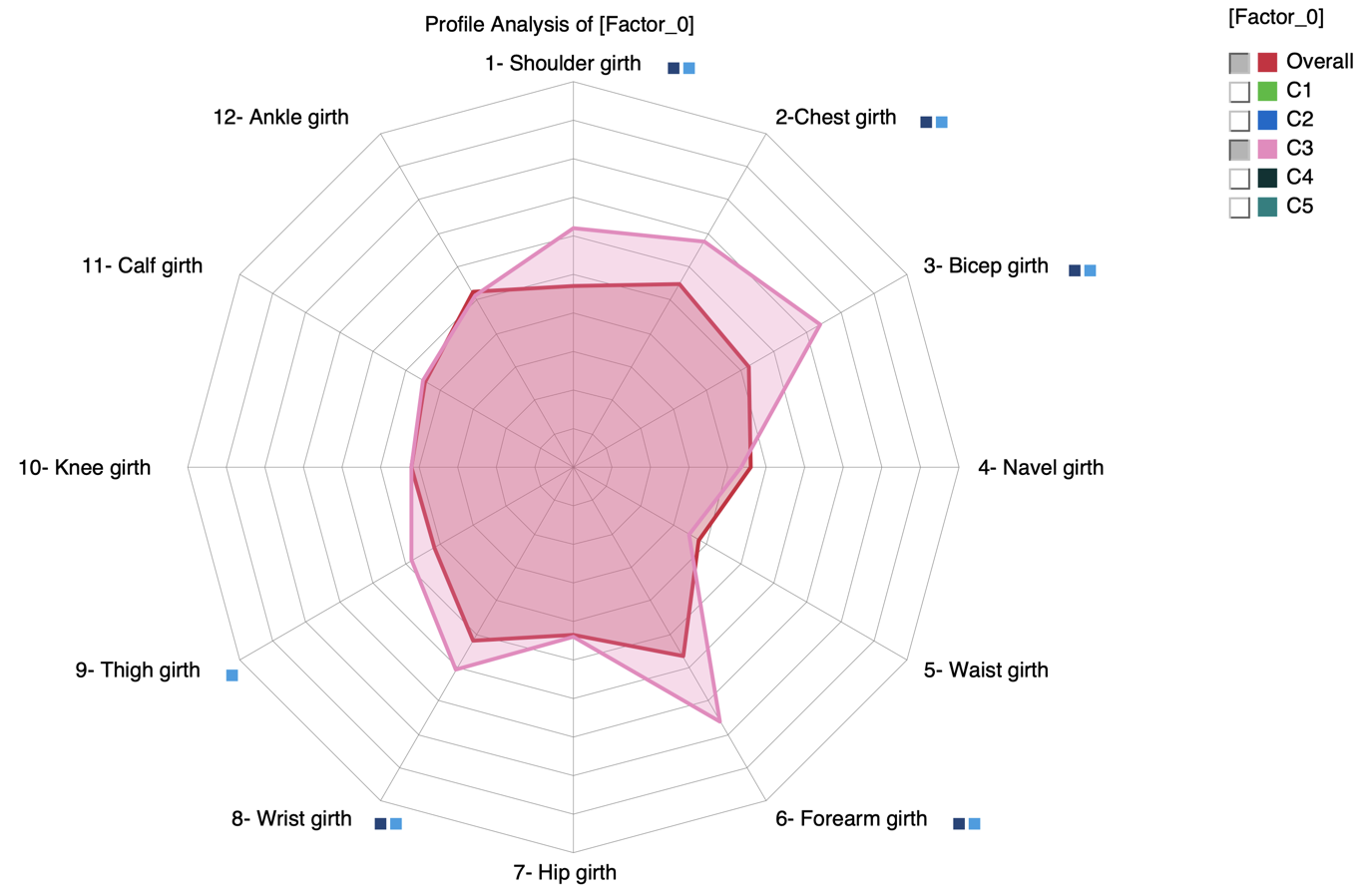
We can also analyze C3 by setting evidence on the measurements. This can be done efficiently by using Histograms (opens in a new tab) (Analysis | Visual | Target | Target's Posterior | Histograms):

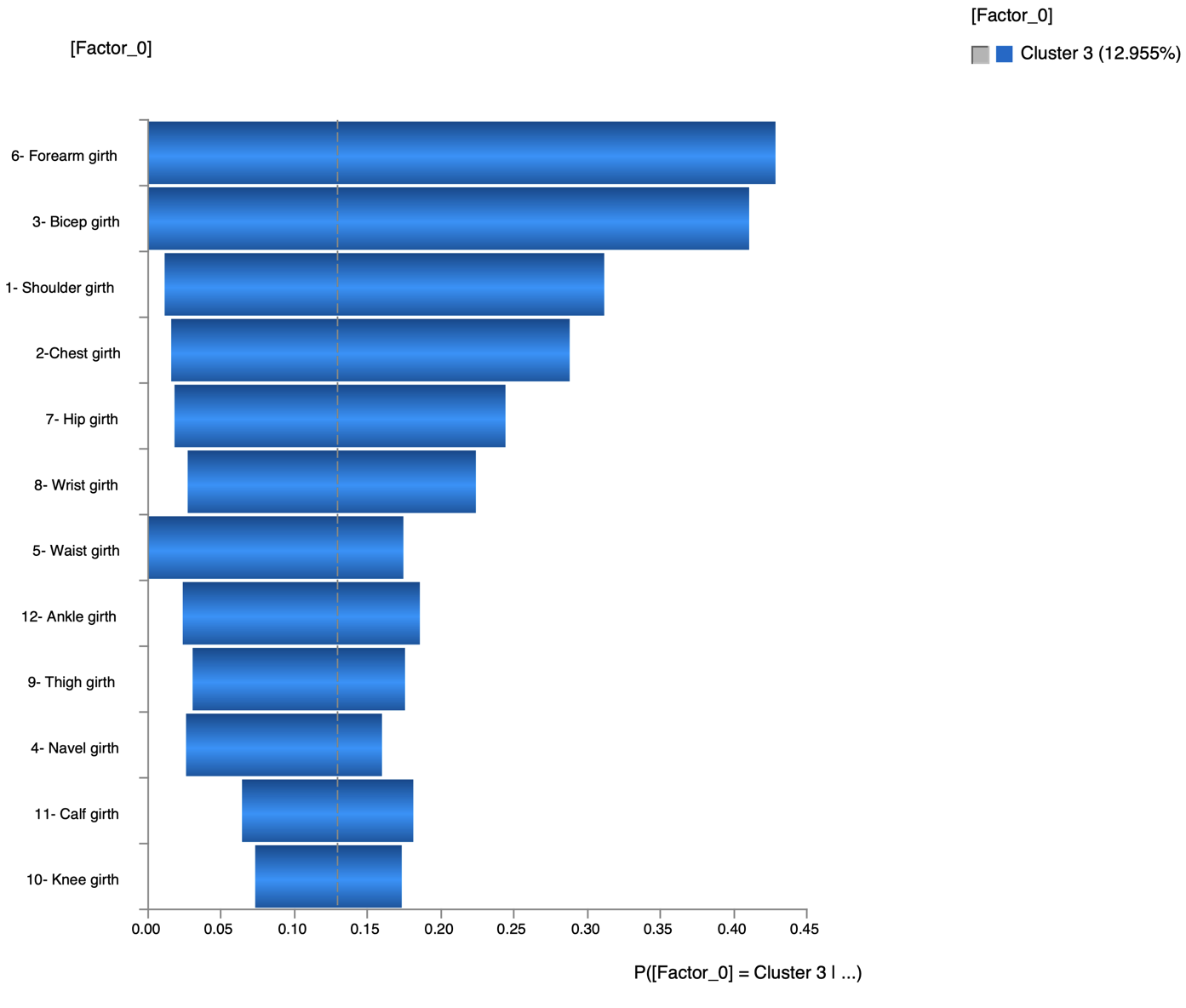
We can also use the Mosaic Analysis (opens in a new tab) (Analysis | Visual | Overall | Mosaic) to get posterior probability distributions of the Target node given each state of the measurements:

where the posterior probability of C3 is represented in blue.

All the previous methods to analyze C3 are based on 1-piece of evidence (either set on the cluster or on the measurements). We can use the BayesiaLab's optimization tools to work with more complex evidence.

The Dynamic Profile (opens in a new tab) is a greedy search algorithm that we can use here to create a profile that describes the men associated with C3:

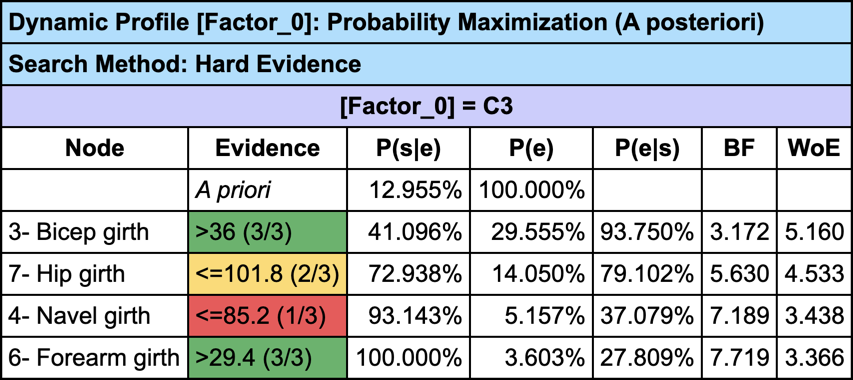
Instead of just using a greedy search for creating the profile of C3, we can use the Target Optimization Tree (opens in a new tab) to create a set of "sketches":

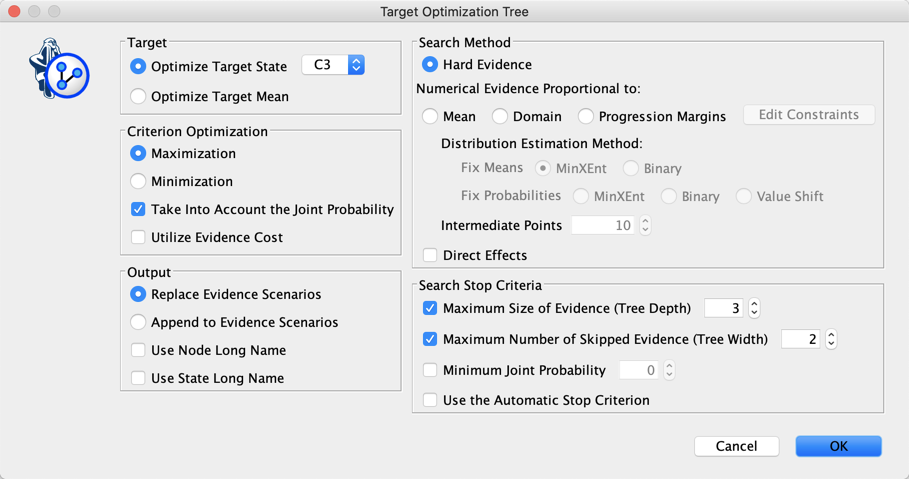
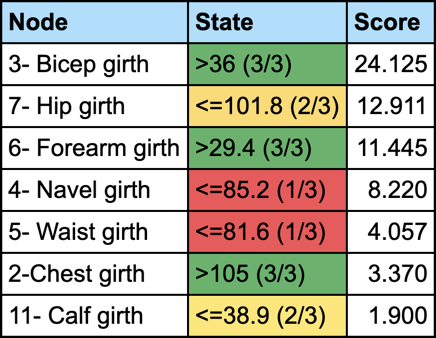
and then generate the report that summarizes the weight of each trait in these sketches:

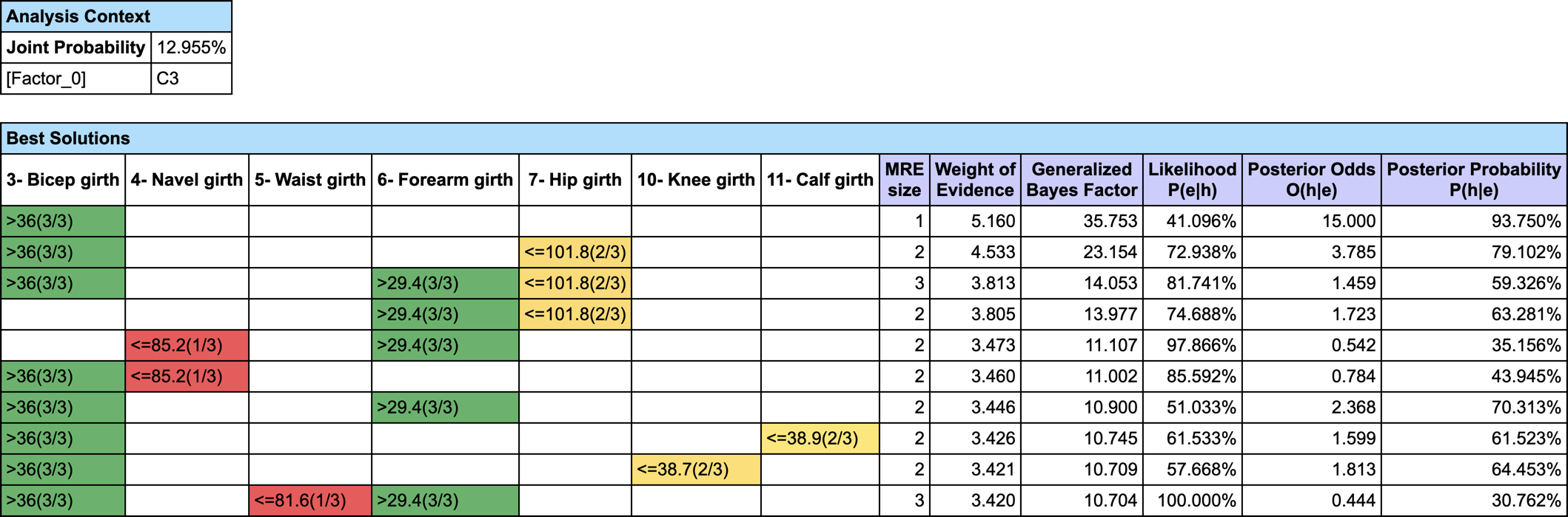
We first set the evidence on C3 and then run Most Relevant Explanations.

The most relevant explanation H* for the evidence is 3- Bicep girth > 36cm (the 3rd and last state)

Since the context of profiling a latent variable is not causal, we interpret the Generalized Bayes Factor with the Odds ratio: the conditional odds of 3- Bicep girth > 36cm given C3 are almost 36 times greater than the marginal odds (15 versus 0.42).

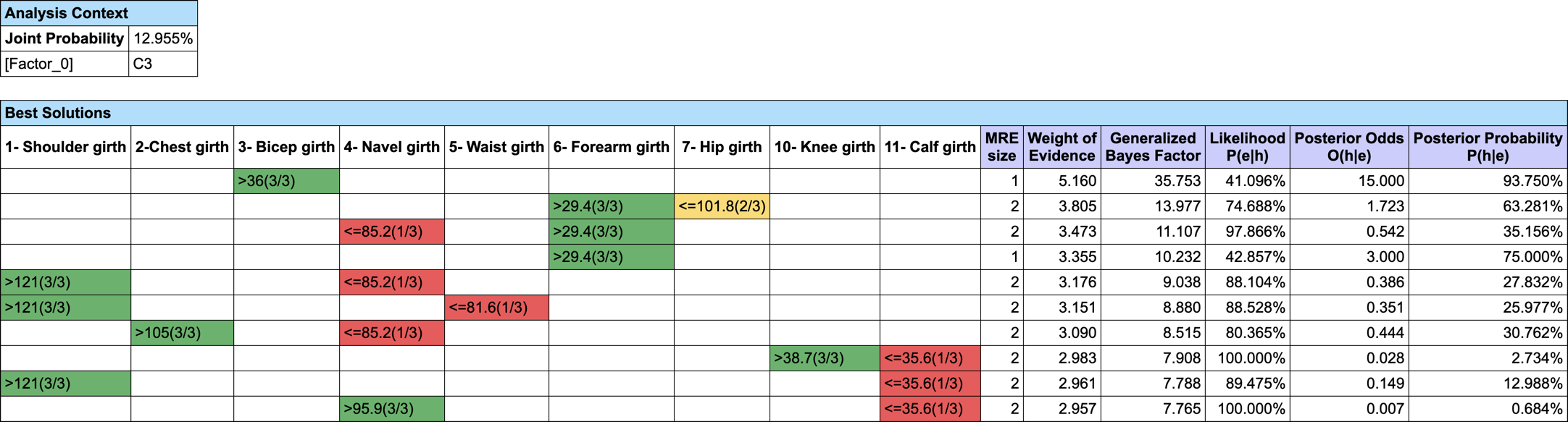
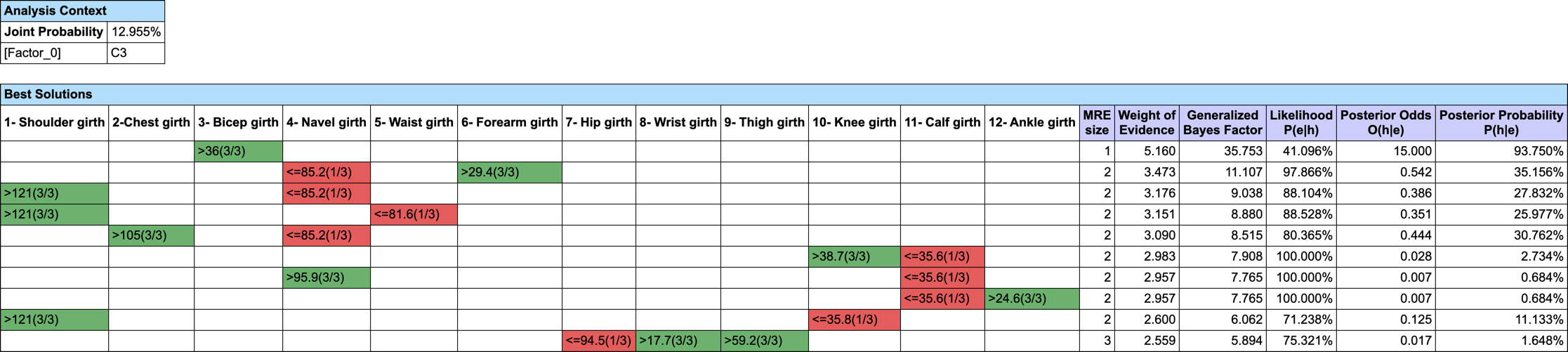
Let's suppose we want to find out what are the triplets of traits that Maximize the A Posteriori given C3. We do not have (yet) a MAP function implemented in BayesiaLab, but we can easily augment our Bayesian network with Function Nodes (opens in a new tab) and use our Genetic Function Optimization (opens in a new tab) tool to find our triplets (Analysis | Function Optimization | Genetic).

#Obs: the number of Hard Evidence set in the network. We can get this number with the Inference Function ObsCount(True, false, false, false),
#ObsMin: the minimum number of Hard Evidence that we set to 4 to search for triplets (i.e. C3 plus the triplets),
Joint: the joint probability of the current set of evidence. It is returned by the Inference Function JointProb(),
MAP: the score we want to maximize, defined with the equation if .

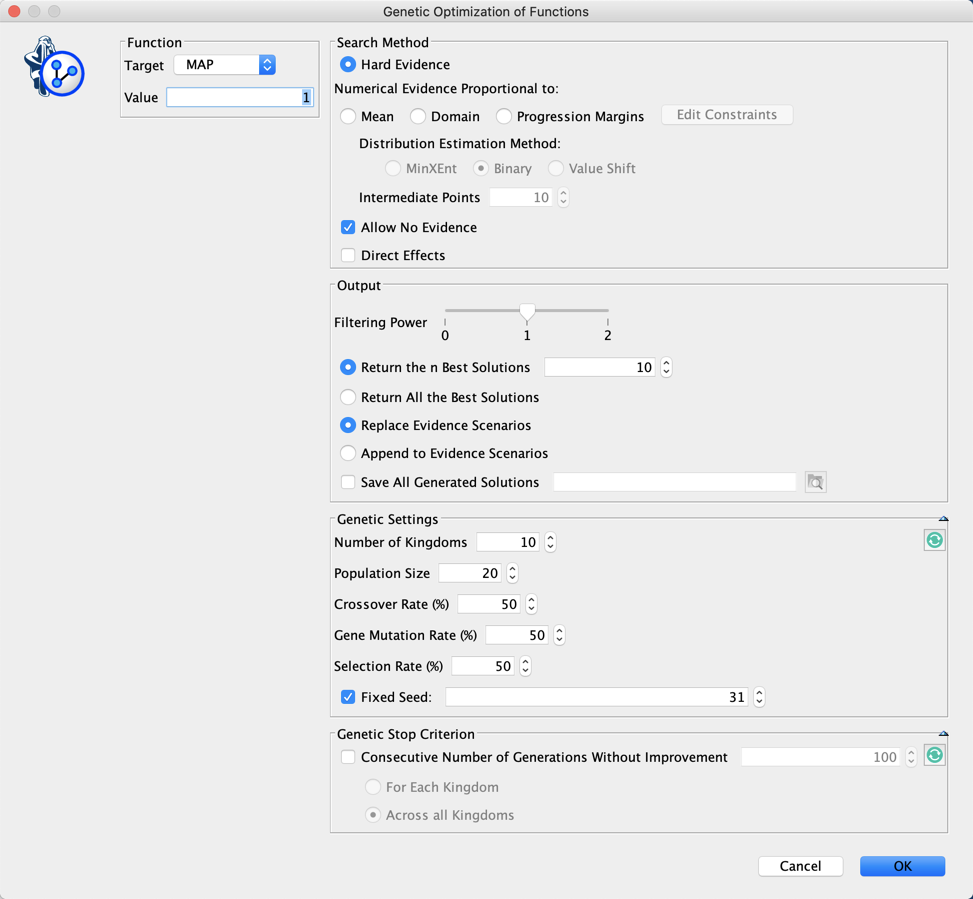
We did not set here any Stop Criterion. This means that we will need to stop the genetic algorithm by clicking in the lower-left corner of the graph window.

The current Best Score is shown at the end of the Progress Bar. You can also see which Generation found this score.

You can also see at the lower right corner of the Graph Panel the icon blinking. This indicates that there are some outputs in the Console (opens in a new tab). Clicking on this icon will open the Console:

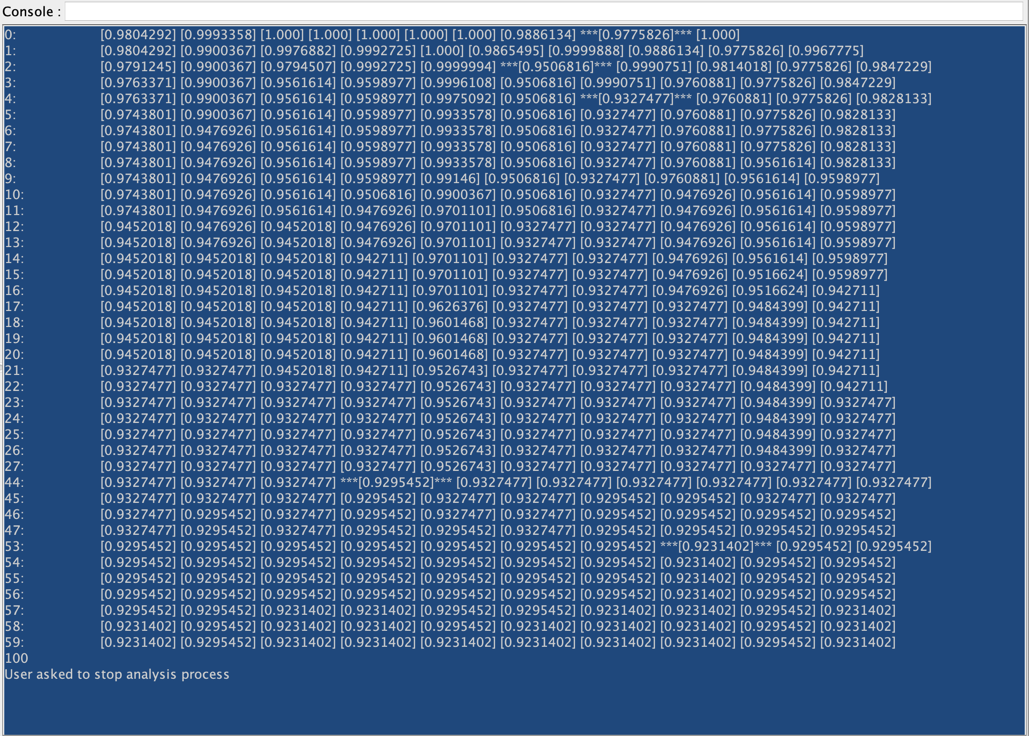
While the first column indicates the Generation, the following columns return the score of the current best individual in each Kingdom. When a score is framed with "***", it indicates that there has been an improvement in this Generation

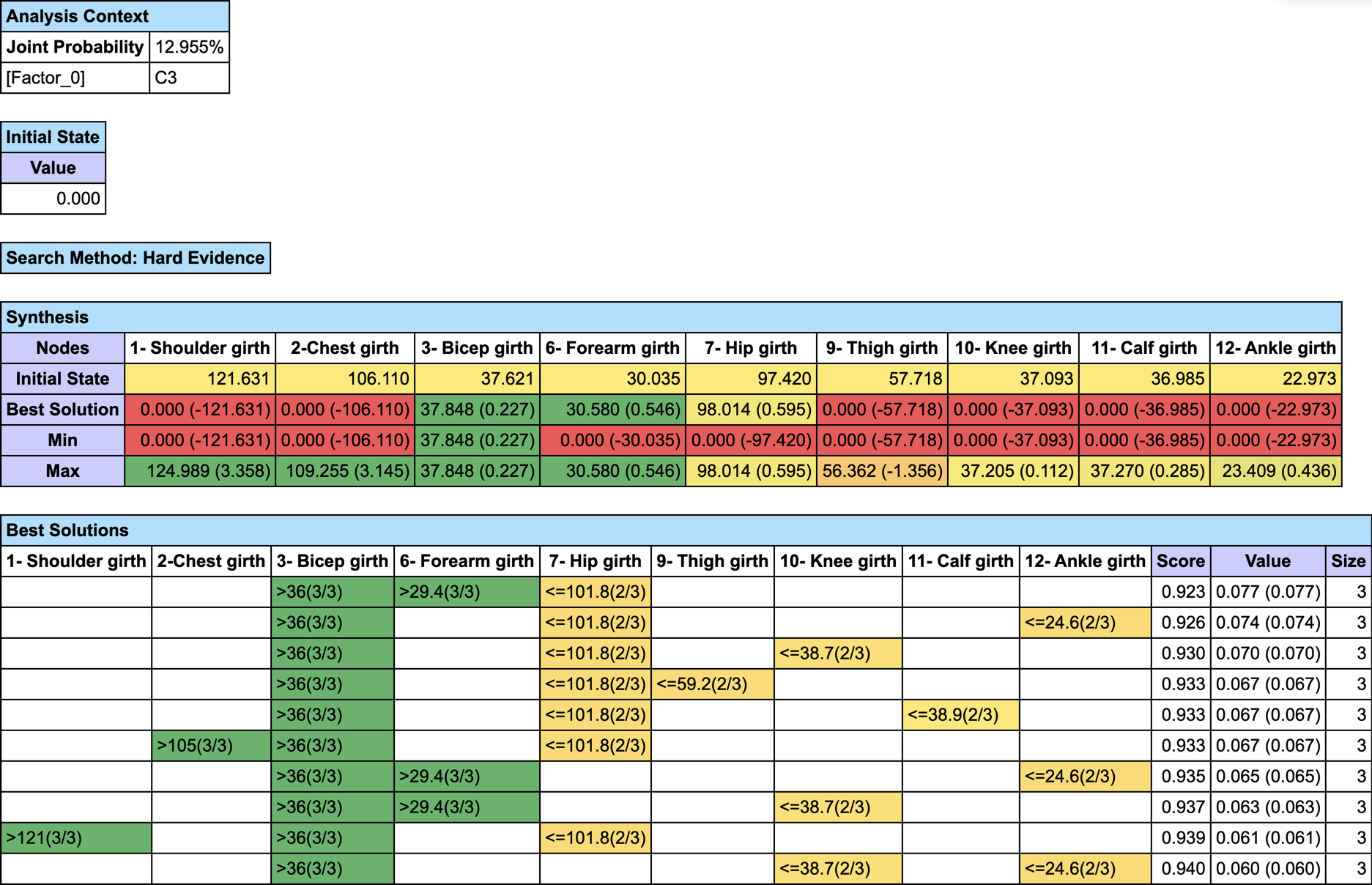
If you want to find out the MAP on a specific subset of nodes, you just have to set #ObsMin to 0, and either select the nodes before running the optimization with "Restrict Search to the Selected Nodes", or set all other nodes as Not Observable.

Here is an image that represents the profile of the men who belong to C3 on the basis of all these analyses:

Information Gain (9.0)Partial Ordering (9.0)