Maximum Weight Spanning Tree

Context

• The Maximum Weight Spanning Tree learning algorithm is by far the quickest Unsupervised Structural Learning Algorithm. It only relies on two passes:
  • The first pass consists of computing the a priori weight of all binary relationships between all variables.
  • The second pass constructs the Maximum Weight Spanning Tree of those relationships.
• While the resulting network may not be optimal, it can be useful for an initial imputation of values as part of a Missing Values Processing strategy.
• The Maximum Weight Spanning Tree learning algorithm can be used as a first network prior to using the Taboo or EQ algorithms.
• Furthermore, it is a practical basis for performing Variable Clustering.
• Internally, the Maximum Weight Spanning Tree initially produces an undirected network. To obtain a directed Bayesian network, BayesiaLab orients the arcs so that V-structures are avoided. However, the presence of Fixed Arcs can lead to the introduction of V-structures.
• The following conditions apply to the Maximum Weight Spanning Tree:
  • Fixed Arcs are not protected from deletion.
  • Any constraints defined through Forbidden Arcs are respected.
  • Temporal Indices are taken into account.

Usage

• Select Menu > Learning > Unsupervised Structural Learning > Maximum Spanning Tree.
• A new window prompts you to specify the learning settings:
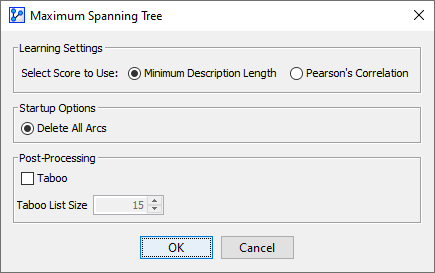
• For this learning algorithm only, you have a choice between two scoring methods, i.e.,
  • Minimum Description Length Score.
  • Pearson's Correlation
• Checking the Taboo box in the Post-Processing panel launches a Taboo search of the specified Taboo List Size in an attempt to improve the network beyond the initial solution found by the Maximum Weight Spanning Tree.
• The principle of the Taboo search is to permit the score to deteriorate, which is normally "taboo", with the objective of finding a better solution beyond the immediate local optimum.