Information Gain (9.0)

Context

Analysis | Report | Evidence | Information Gain

The Log-Loss LL(E) reflects the cost to process a particle E with a model, i.e. the number of bits that are needed to encode the particle E given the model. The lower the probability is, i.e. the more surprising a particle is given our model, the higher the log-loss is.

where P(E) is the joint probability of the n-dimensional evidence E returned by the Bayesian network:

The Information Gain is the difference between the cost to process a particle E with the fully unconnected network (the straw model S, where all nodes are marginally independent), and the cost with the current Bayesian network B:

History

This function, previously called Evidence Analysis Report (opens in a new tab), has been first updated in version 5.0.2 (opens in a new tab).

Renamed Metrics: Local Information Gain

The metric used to compare the cost to represent the posterior probability of the 1-piece of hypothetical evidence h given the current set of evidence E and its prior probability is now called Local Information Gain instead of Information Gain.

Renamed Metrics: Hypothetical Information Gain

What would be the Information Gain if h, a 1-piece of evidence, were added to the current set of evidence E? This metric was called Bayes Factor in the previous releases.

New Feature: Analysis of the Selected Nodes Only

As of version 9.0, the analysis can be carried out on the selected nodes only.

Example

Let's use the network below with the following 3-pieces of evidence E:

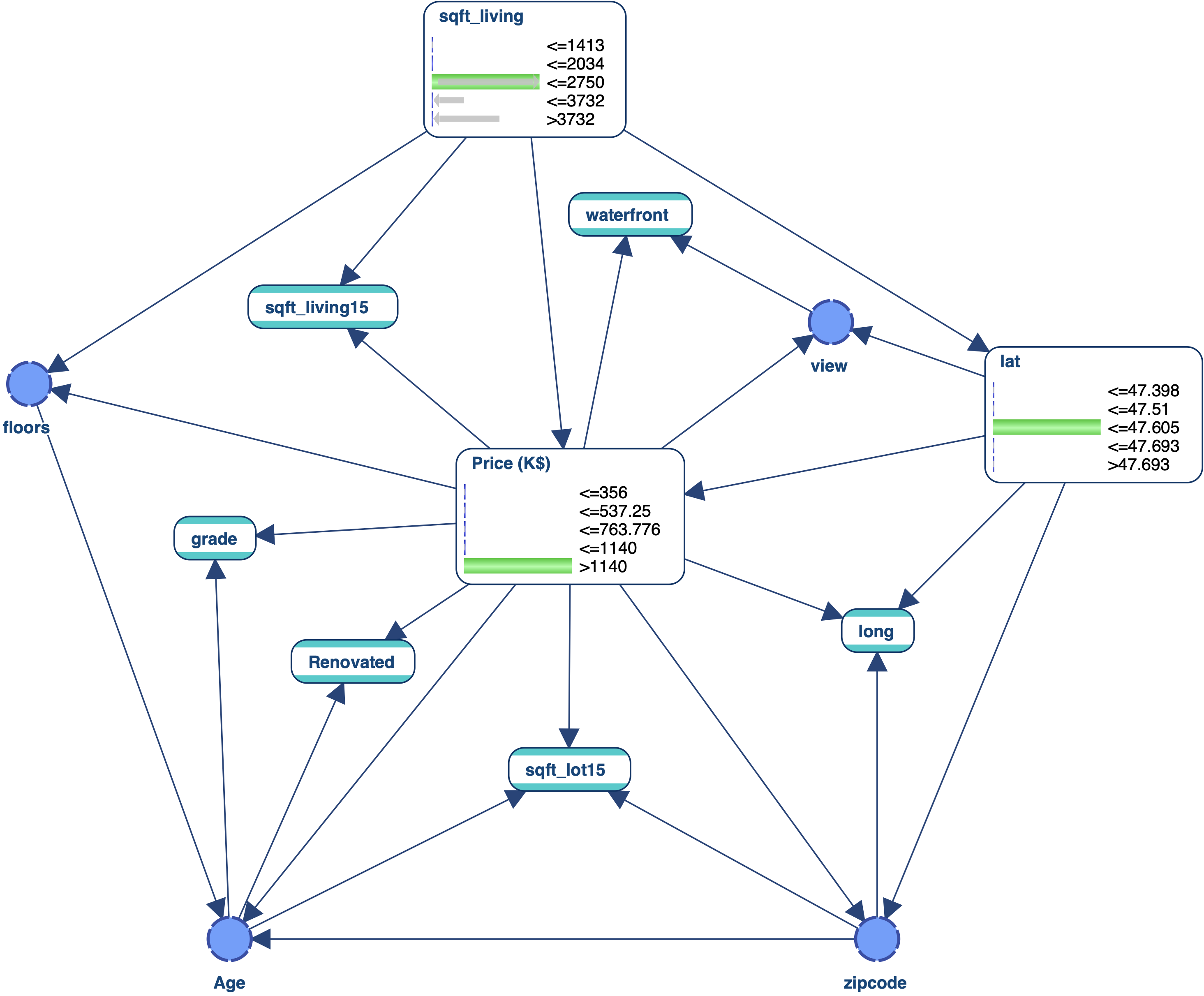
We select _**waterfront, view, Age, Renovated, and grade and run the analysis on these 5 nodes only:

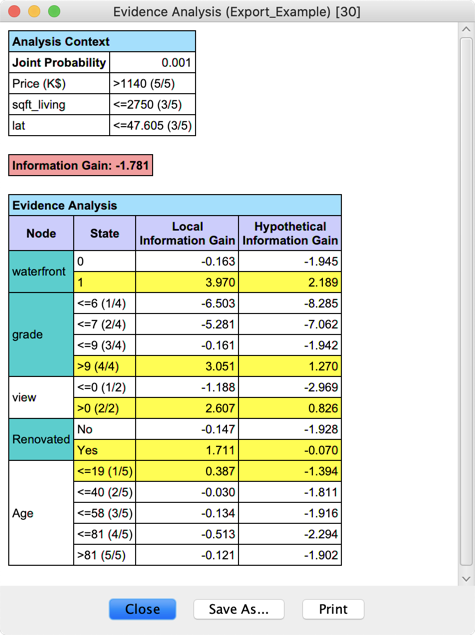
As we can see, the Information Gain of E with this network is negative (-1.781). A negative Information Gain is sometimes called a Conflict.

However, if we were to add the evidence waterfront = 1, this would make the Information Gain of the new 4-piece of evidence positive (2.189). These 4 observations are occasionally qualified as Consistent with our network.