Confidence Intervals Analysis
Context
- The Confidence Intervals Analysis helps interpret a wide range of metrics relating to nodes in a Bayesian network.
- In many of BayesiaLab’s reports, such as the Target Analysis Report, quantities are displayed as single-point estimates, for instance, the mean value of a node, or the Mutual Information between two nodes.
- When comparing such values between several nodes, single-point estimates are not enough to judge as to which node is higher in value or more important.
- Importantly, we need to take into account the uncertainty associated with any estimates, regardless of whether the uncertainty comes from assessments or from a small sample size.
- Before we explain the workflow for the Confidence Intervals Analysis, we need to take a step back to recapitulate the Confidence Intervals Report.
Confidence Intervals Report
- To run the Confidence Intervals Report go to
Menu > Network > Reports > Confidence Intervals.-
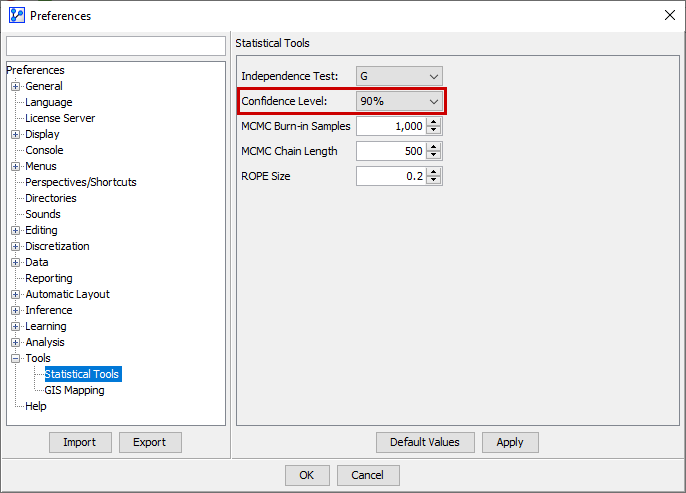
For BayesiaLab to construct the desired Confidence Intervals, you need to specify a Confidence Level in Preferences.
-
Go to
Menu > Window > Preferences > Tools > Statistical Tools. -
Select the desired value from the Confidence Level dropdown menu.
-
For example, if you specify a Confidence Level of 90%, it means that BayesiaLab constructs the Confidence Intervals so that there is a 90% probability that the true parameter value falls within the Confidence Intervals of the parameter estimate .
-
Note that your selection of the Confidence Level also applies to all other statistical tools and tests used in BayesiaLab, including the Confidence Intervals Analysis explained below.
-
Confidence Intervals Analysis
- To start the Confidence Intervals Analysis, go to
Menu > Analysis > Visual > Sensitivity > Confidence Intervals. - The Confidence Intervals Analysis constructs the Confidence Intervals exactly the same way the Confidence Intervals Report described above.
- This process is conceptualized in the following diagram. It shows the probability densities of the parameter estimates.
Monte Carlo Simulation
-
Next, BayesiaLab performs a Monte Carlo Simulation by sampling probabilities from the constructed Confidence Intervals and creating a Bayesian network for each sample.
-
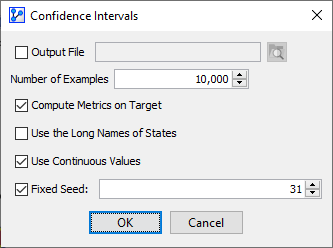
In this context, you need to specify the number of samples BayesiaLab draws from the parameter distributions for generating the corresponding Bayesian networks.
-
Setting a value of 10,000 means that BayesiaLab will generate 10,000 Bayesian networks with parameters sampled from the Confidence Intervals.
-
Then, these 10,000 networks are evaluated in terms of how the sampled parameters affect the Joint Probability Distribution.
-
The Confidence Intervals Analysis Report calculates the following items:
- States’ Probabilities
- Mean
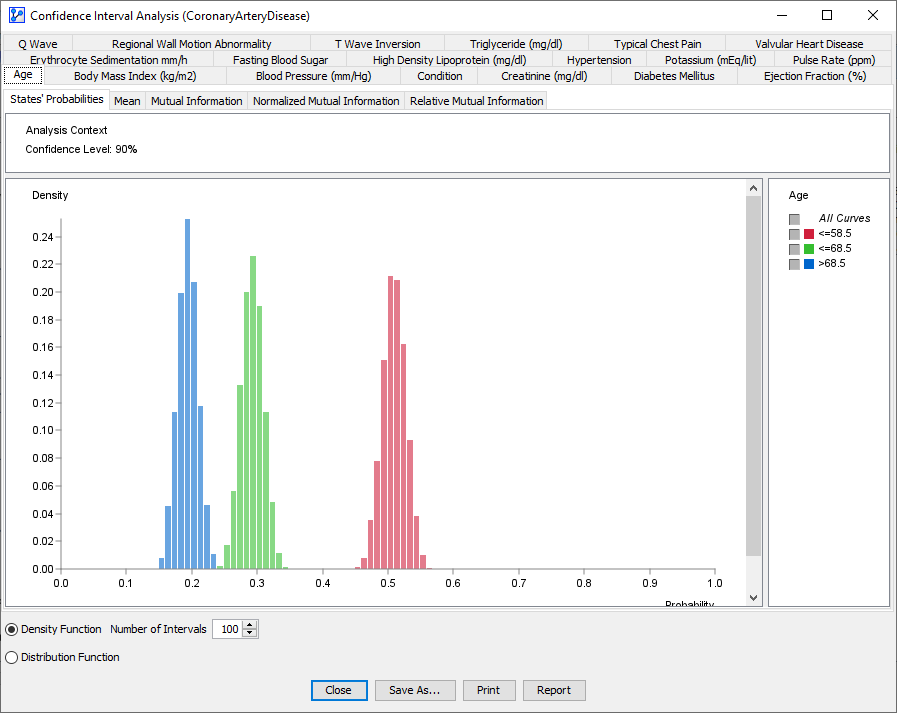
- The screenshot shows the distributions of the State Probabilities of the node Age.
-
Furthermore, if the network contains a Target Node, and you set the Compute Metrics on Target option, BayesiaLab also computes the following metrics for each node with regard to the Target Node.
- Mutual Information
- Normalized Mutual Information
- Relative Mutual Information
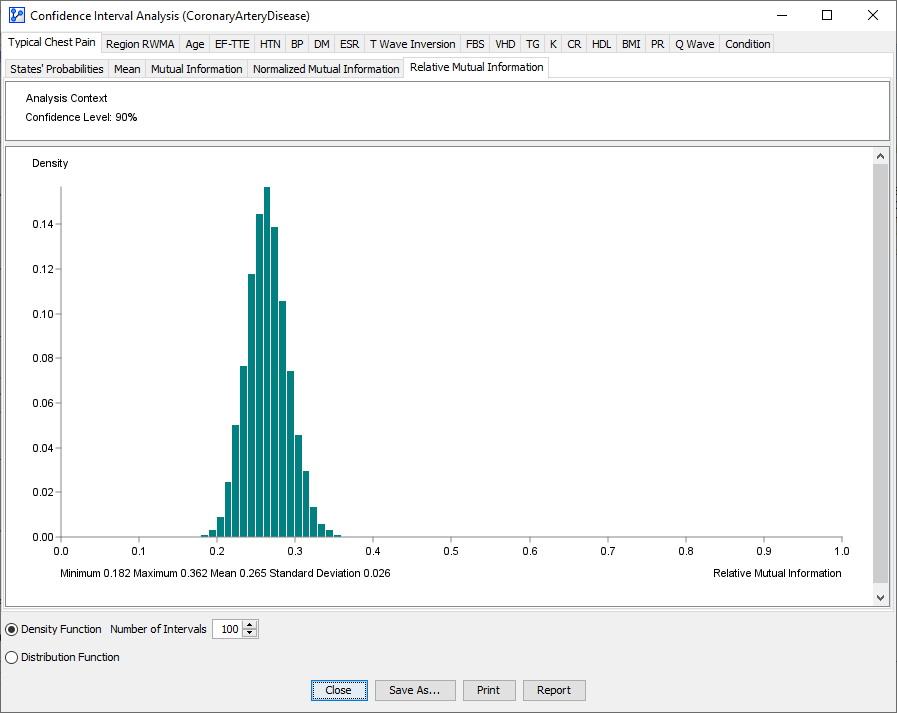
- The following screenshot shows the distribution of Relative Mutual Information of the node Typical Chest Pain with regard to the Target Node Condition.
 —>
—>
Workflow Illustration
-
To demonstrate this workflow, we use the Coronary Artery Disease network, which you can download here:
CoronaryArteryDisease.xbl -
In this example, we run the Confidence Intervals Analysis on all nodes.
-
Next, we select Relative Mutual Information as the metric of interest and sort the tabs accordingly.
-
Each tab at the top of the window represents one node in the network.
-
As we click through the tabs from left to right, we observe that the Relative Mutual Information decreases.
-
This is in sync with what we would obtain from a Target Analysis Report
Menu > Analysis > Report > Target > Relationship with the Target Node. -
We show the corresponding report here just for reference:
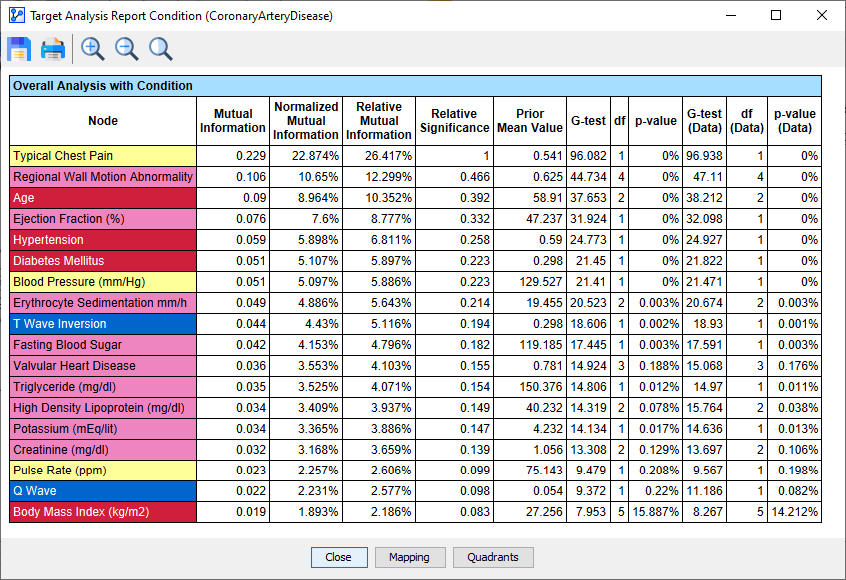
-
We may now be tempted to read this report as a hierarchy in terms of importance.
-
However, we need to be careful about such conclusions. The following animation highlights the issue:
-
By overlaying the distributions of the Relative Mutual Information values, we can only find that Typical Chest Pain is clearly distinct from the remaining nodes.
-
The Relative Mutual Information distributions of the remaining nodes seem to blend into each other, which implies that the hierarchy the Target Analysis Report above suggests isn’t nearly as clear.
-
As a result, we need to be careful with any claims regarding a rank order of the nodes unless the Confidence Interval Analysis demonstrates clearly separated distributions.

