Infer — Dynamic Imputation
Dynamic Imputation is the first of a range of methods that take advantage of the structural learning algorithms available in BayesiaLab.
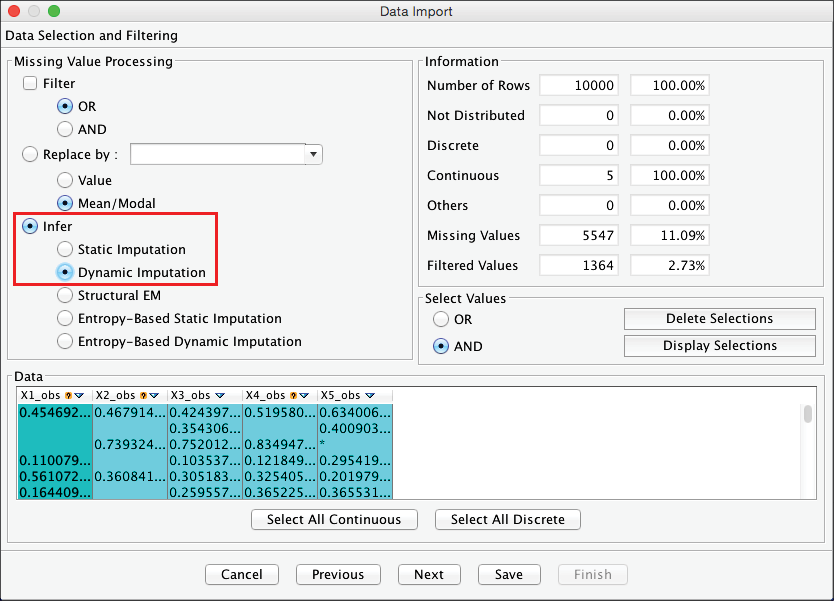
Like Infer — Static Imputation, Dynamic Imputation is probabilistic; imputed values are drawn from distributions. However, unlike Infer — Static Imputation, Dynamic Imputation does not only perform imputation once but rather whenever the current model is modified, i.e., after each arc addition, deletion, and reversal during structural learning. This way, Dynamic Imputation always uses the latest network structure for updating the distributions from which the imputed values are drawn.
Upon completion of the data import, the resulting unconnected network initially has exactly the same distributions as the ones we would have obtained with Static Imputation. In both cases, imputation is only based on marginal distributions. With Dynamic Imputation, however, the imputation quality gradually improves during learning as the structure becomes more representative of the data-generating process. For example, a correct estimation of the MAR variables is possible once the network contains the relationships that explain the missingness mechanisms.
Dynamic Imputation might also improve the estimation of MNAR variables if structural learning finds relationships with proxies of hidden variables that are part of the missingness mechanisms.
The question marks associated with X1_obs, X2_obs, and X4_obs confirm that the missingness is still present, even though the observations have been internally imputed.
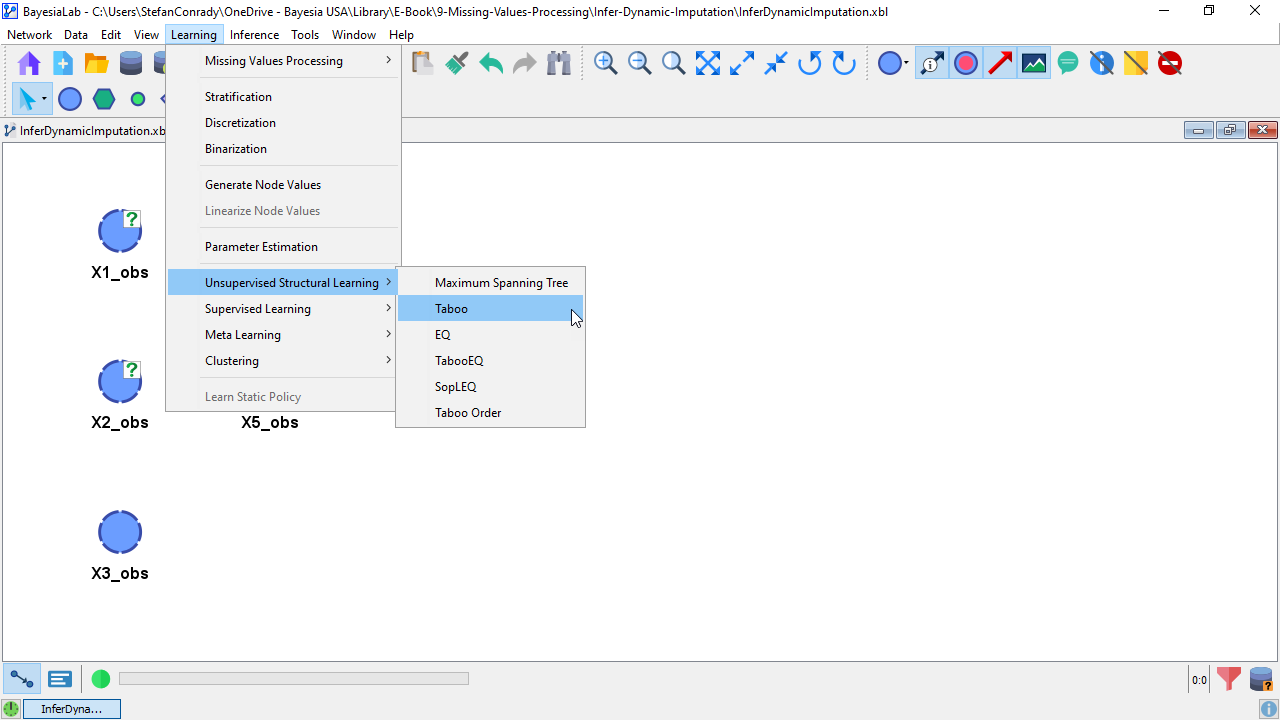
On the basis of this unconnected network, we can perform structural learning. We select Menu > Learning > Unsupervised Structural Learning > Taboo.
While the network only takes a few moments to learn, we notice that it is somewhat slower compared to what we would have observed using a non-dynamic missing values processing method, e.g., Filter (Listwise/Casewise Deletion), Replace By (Mean/Modal Imputation), or Infer — Static Imputation. For our small example, the additional computation time requirement is immaterial. However, the computational cost increases with the number of variables in the network, the number of missing values, and, most importantly, the complexity of the network. As a result, Dynamic Imputation can slow down the learning process significantly.
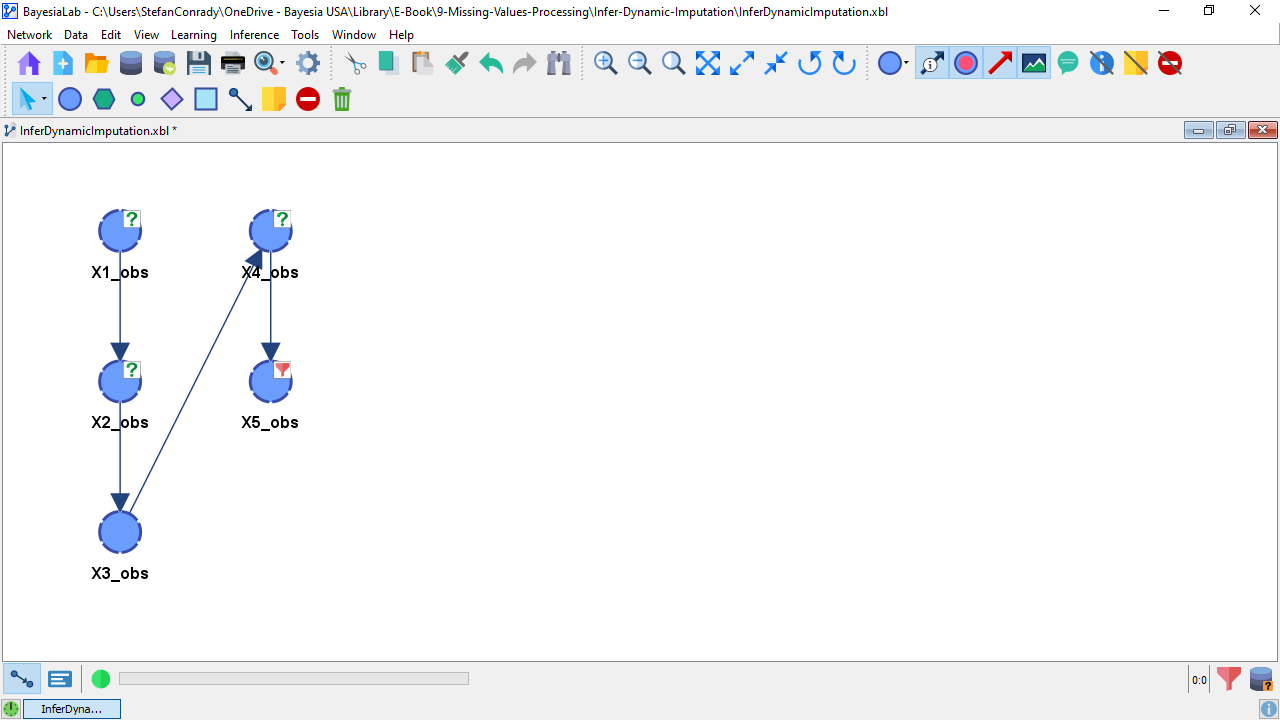
The following screenshot reports the performance of the Dynamic Imputation. The distributions show a substantial improvement compared to all the other methods we have discussed so far. As expected, X2_obs is now correctly estimated, and it even improves the distribution estimation of the difficult-to-estimate MNAR variable X4_obs. More specifically, there is now much less of an underestimation of the mean value.
