Skip to Content
BayesiaLabBayesiaLab User GuidePanelsNode EditorNode Editor — Probability DistributionsFormulaContinuous Probability Distributions

Continuous Probability Distributions

Normal(x, m, s)

  • Description: Normal distribution of x with mean m and standard deviation s.

  • Number of parameters: 3

  • Parameter type: numerical, numerical, numerical

  • Result type: real

Example

The probability distribution below corresponds to Normal(?N1?, 0.3, 0.1):

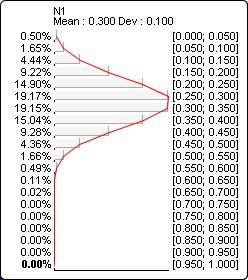
3407883

Triangular(x, m, l, r)

  • Description: Triangular probability distribution of x with modal value m, left deviation l, and right deviation r.

  • Number of parameters: 4

  • Parameter type: numerical, numerical, numerical, numerical

  • Result type: real

Example

The probability distribution below corresponds to Triangular(?N1?, 0.5, 0.2, 0.4):

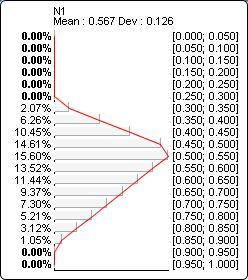
3407884

Cauchy(x, m, s)

  • Description: Cauchy probability distribution of x with modal value m and scale s.

  • Number of parameters: 3

  • Parameter type: numerical, numerical, numerical

  • Result type: real

Example

The probability distribution below corresponds to Cauchy(?N1?, 0.5, 0.1):

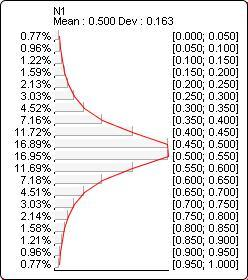
3407886

Exponential(x, l)

  • Description: Exponential probability distribution of x with lambda = l.

  • Number of parameters: 2

  • Parameter type: numerical, numerical

  • Result type: real

Example

The probability distribution below corresponds to Exponential(?N1?, 2):

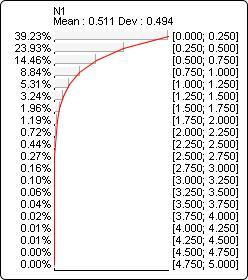
3407888

Weibull(x, a, l)

  • Description: Weibull probability distribution of x. Note that Weibull(x, 1, l) = Exponential(x, l).
  • Number of parameters: 3
  • Parameter type: numerical, numerical, numerical
  • Result type: real

Example

The probability distribution below corresponds to Weibull(?N1?, 1.5, 1.5):

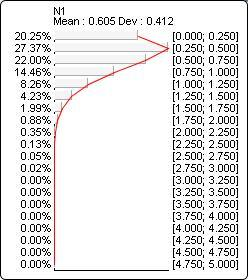
3407889

Gamma(x, a, l)

Density:

f(x,a,l)=xa−1e−xlΓ(a)laf(x,a,l) = \frac{{x^{a - 1} e^{ - \frac{x}{l}}}}{{\Gamma(a) l^a}}
  • Description: Gamma probability distribution of x. Gamma(x, 1, l) = Exponential(x, l).
  • Number of parameters: 3
  • Parameter type: numerical, numerical, numerical
  • Result type: real

Example

The probability distribution below corresponds to Gamma(?N1?, 1.5, 1.5):

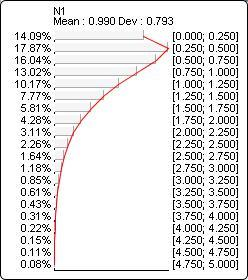
3407890

Beta(x, a, b, bi, bs)

  • Description: Beta probability distribution of x. The last two parameters represent the lower and upper bounds of the variable, with default values 0 and 1.
  • Number of parameters: 5
  • Parameter type: numerical, numerical, numerical, numerical, numerical
  • Result type: real

Example

The probability distribution below corresponds to Beta(?N1?, 2, 5, 0, 5):

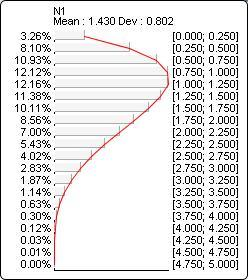
3407891

ChiSquare(x, n)

  • Description: Chi-Square probability distribution of x with n degrees of freedom.
  • Number of parameters: 2
  • Parameter type: numerical, integer
  • Result type: real

Example

The probability distribution below corresponds to ChiSquare(?N1?, 3):

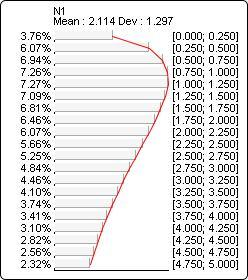
3407892

LogNormal(x, m, s)

  • Description: Log-normal probability distribution of x.
  • Number of parameters: 3
  • Parameter type: numerical, numerical, numerical
  • Result type: real

Example

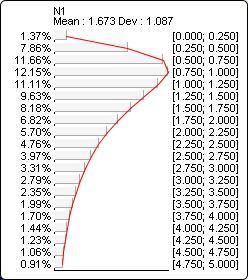
The probability distribution below corresponds to LogNormal(?N1?, 0.4, 0.8):

3407893

Uniform(x, a, b)

  • Description: Uniform probability distribution of x on the interval [a, b].
  • Number of parameters: 3
  • Parameter type: numerical, numerical, numerical
  • Result type: real
ConstantsDiscrete Probability Distributions