Symmetric Normalized Mutual Information

Context

The following Venn Diagram illustrates that the Mutual Information is symmetrical for the two variables $X$ and $Y$ , i.e., $I(X,Y)=I(Y,X)$ .

However, the variables $X$ and $Y$ can each have a different number of states. Therefore, their respective entropies can be very different.

This means that the absolute value of Mutual Information cannot be interpreted without context. In the Venn Diagram, for instance, $I(X|Y)$ reduces $H(Y)$ by a bigger percentage than does $H(X)$ . As such, $I(X,Y)$ would be more "important" with regard to $Y$ than it would be with regard to $X$ .

Definition

The Symmetric Normalized Mutual Information measure takes the difference of the respective entropies of X and Y into account:

{I_{SN}}(X,Y) = 2 \times \frac{{I(X,Y)}}{{{{\log }_2}({S_X}) + {{\log }_2}({S_Y})}}

As a result, we have an easy-to-interpret measure that relates to both $X$ and $Y$ together.

Usage

For a given network, BayesiaLab can report the Symmetric Normalized Mutual Information in several contexts:

Menu > Analysis > Report > Relationship Analysis:

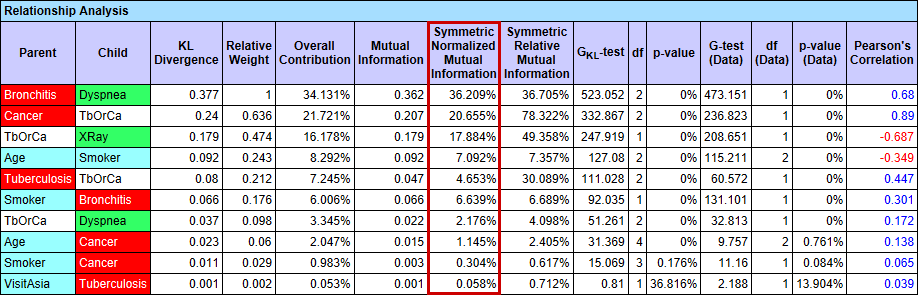
The Symmetric Normalized Mutual Information can also be shown by selecting Menu > Analysis > Visual > Overall > Arc > Mutual Information and then clicking the Show Arc Comments icon or selecting Menu > View > Show Arc Comments.

Note that the corresponding options under Menu > Preferences > Analysis > Visual Analysis > Arc's Mutual Information Analysis have to be selected first:

In Preferences, Child refers to the Relative Mutual Information from the Parent onto the Child node, i.e., in the direction of the arc.
Conversely, Parent refers to the Relative Mutual Information from the Child onto the Parent node, i.e., in the opposite direction of the arc.

Relative Mutual Information Symmetric Relative Mutual Information