Total Effect vs. Direct Effect

Simpson's Paradox Revisited

Why are we using the term “Direct Effect” instead of “causal effect,” which is obviously what we are looking for? It helps to recall the Simpson’s Paradox example from the previous chapter. Through path analysis, we were able to distinguish between causal (blue ) and non-causal paths (pink ). We argued that the arc $X → Y$, i.e., the direct causal path, represents the causal effect. By adjusting for $Z$ and thus blocking the non-causal path $X ← Z → Y$, we were able to isolate the “direct effect” of $X$ on $Y$. However, if had we not adjusted for $Z$, both the causal and the non-causal path would remain open, and we would obtain the “total effect.” This is indeed the nomenclature we follow in BayesiaLab.

By invoking Direct Effect, BayesiaLab will automatically perform Likelihood Matching on all Confounders and estimate the causal effect.

Direct Effect

To emphasize the distinction between Direct Effect and Total Effect, we look one more time at Simpson’s Paradox (SimpsonsParadox.xbl (opens in a new tab)).

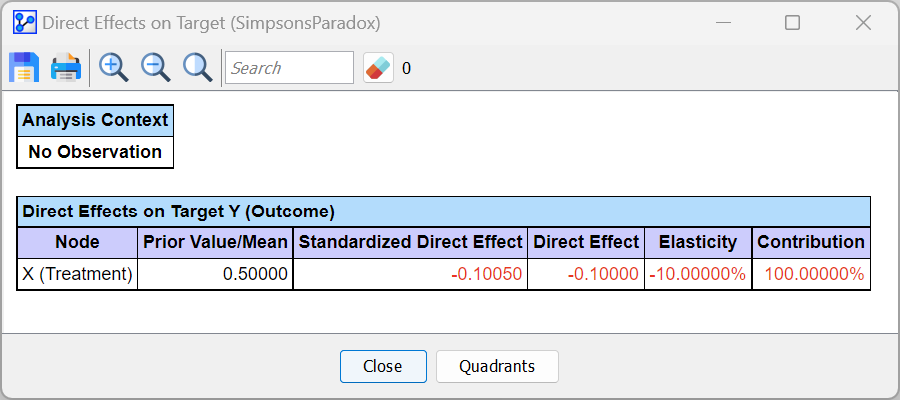
• Click X and then select Menu > Analysis > Report > Target Analysis > Direct Effects on Target.

We immediately obtain a report that shows a Direct Effect of −0.1. This value is identical to the Average Treatment Effect we computed in the previous chapter. As expected, adjustment by stratification, Graph Surgery, and Likelihood Matching provides the same effect estimate.

Total Effect

For comparison, we now estimate the Total Effect:

• Select Menu > Analysis > Report > Target Analysis > Total Effects on Target.

The resulting report window now shows the Total Effect, which amounts to +0.1.

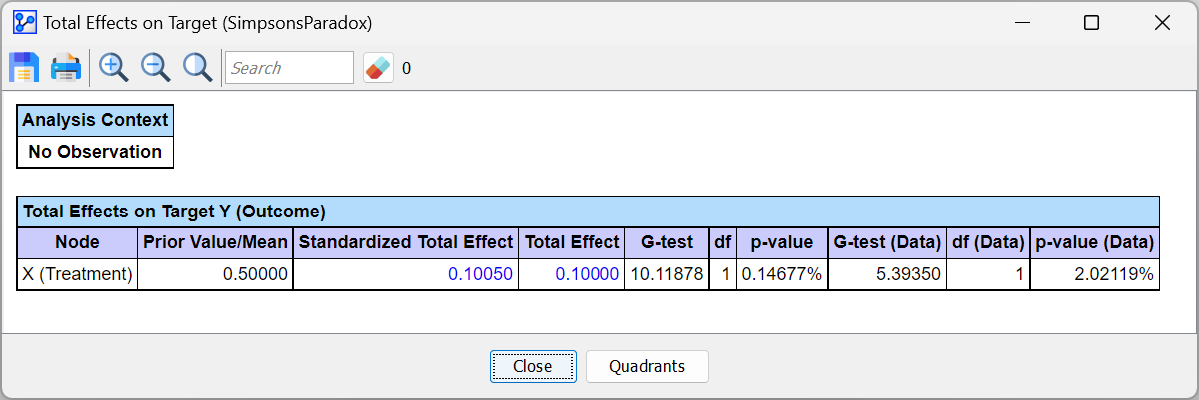
This result matches the naive estimator, i.e., the effect we observe when considering the whole population, which is clearly not the causal effect. So, why would we need to estimate the Total Effect at all? It would be the only correct estimator for performing observational inference, i.e., prediction. If we were merely observing treated versus not treated patients instead of performing an intervention, the Total Effect provides the expected change of the outcome variable.