Example: Most Relevant Explanations for Failure Analysis

Example Background & Context

• To illustrate the Most Relevant Explanations function, we present a causal Bayesian network derived from a problem domain explained in Yuan, C. et al. (2011) (opens in a new tab), which had originally been proposed in Poole, D., & Provan, G. M. (1991).
• This domain was originally described as an electrical circuit consisting of an Input, an Output, plus four switches, A, B, C, and D, which can fail.

Overhead Catenary System

• We took the liberty of embedding this exact problem that Yuan described into a practical technical context, hoping to make it easier to understand.
• So, instead of a fictional and abstract circuit, we are considering an overhead catenary system that supplies power to electric locomotives along railroad tracks.

Conceptual Illustration

• Our system consists of the following elements, as illustrated in the above diagram.
  • A high-voltage wire, a so-called overhead catenary, serves as a power source for electric locomotives.
  • This high-voltage wire is suspended from a support structure that is attached to steel pylons alongside the railroad track.
  • Beyond supporting the wire, this structure must also provide electrical insulation.
  • It does so through four insulators, labeled A, B, C, and D, so that there is no path along which electricity could flow into the steel pylon and ultimately into the ground.
  • As with all equipment that is exposed to the elements and subject to mechanical and electrical forces, these insulators can fail.
  • Long-term operational data has established specific failure probabilities for each of the insulators within a given time period:
    • p(A=defective)=1.6%
    • p(B=defective)=10%
    • p(C=defective)=15%
    • p(D=defective)=10%
  • In this context, "defective" means the degradation from a perfect insulator (R=∞) to an Ohmic resistor (R>>0Ω), not necessarily a short circuit (R=0Ω).
  • As a result, the failure of one or more insulators could create a stray current between the catenary wire ("Input") and the steel pylon anchored in the ground ("Output"), therefore "leaking" electric energy.
  • With that, the overall objective must be to prevent any stray currents. However, our specific objective in this example is to find the relevant causes, if a stray current were to be observed.

Equivalent Circuit

• We can simplify the technical diagram from above into the following equivalent pseudo circuit, in which we represent the real-world insulators as idealized switches:

  • The equivalent of a functioning insulator is an open switch.
  • The equivalent of a defective insulator is a closed switch.
  

• Note that this circuit representation is identical to the one Yuan's paper.

• Looking at the arrangement of the insulators/switches, we can see that not all failures have the same effect:

  • A failure of A would immediately create a connection between the Input and the Output, leading to a power drain.
  • However, if any one of B, C, or D failed by themselves, it would not create an immediate problem.

• Beyond nodes that represent actual, technical components in our system, we introduce intermediate output nodes that inform us about the conditions on the output sides of the switches/insulators.

• Think of these intermediate output nodes as embedded sensors that indicate whether the corresponding switch can transmit power to the point where sensors are attached.

• Here,  the equivalent pseudo circuit is shown with the intermediate output nodes in place:

Explanatory Causal Bayesian Network

• Now we have all the elements we need to represent this domain in a causal Bayesian network:
  • Input (i.e., the catenary) has the states, Power and No Power.
  • Output (i.e, the pylon) has the states Current and No Current.
  • The node names for the switches (i.e., the insulators) correspond to their designation in the diagram, i.e., A, B, C, and, D. They all feature the states OK and defective.
  • The node names for the intermediate output nodes are Output A through Output D. Each of them has the states Power and No Power, indicating where the respective switch can transmit power or not.
• Upon entering the failure probabilities, we have a fully specified causal Bayesian network, which you can download here:
  Yuan_Lu_Circuit.xbl

Initial State of Bayesian Network 

• Assuming that Input=Voltage, we can see how the Bayesian network computes the probability of Output=Current, i.e., the presence of a stray current.

System Failure Observed

• However, we are going to change the viewpoint. Instead of predicting the probability of system failure, we actually do observe a system failure, i.e., we measure a stray current that is flowing all the way through to the Output.
• So, one or more of the components in this system must have failed.
• Unfortunately, we do not have access to the intermediate outputs, which would reveal what the problem is. Note that those nodes are marked as Not Observable .
• So, we must infer from the observed outcome and reason back to the potential causes.
• More specifically, we wish to know the most relevant causes, i.e., what would best explain the outcome we have observed.
• The following network illustrates the status of all nodes after setting Output=Current.
  
• Naively, we might expect that the node with the highest probability of being defective is the one that prompted the failure.
• However, the question is much more complex than that.

Most Relevant Explanations

• We need to employ the Most Relevant Explanations feature to identify the problems.
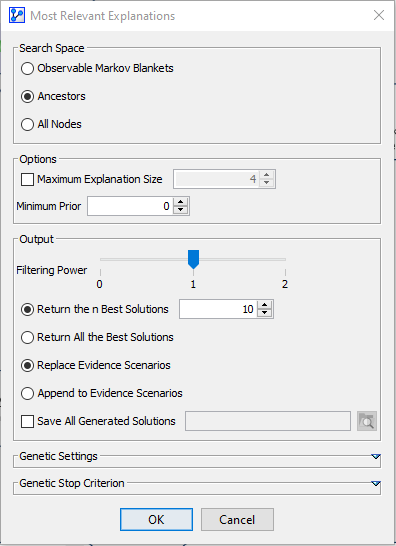
• Select Analysis > Report > Evidence > Most Relevant Explanations.
• This opens up an options window, in which we the Search Space to the Ancestors of the Target Node Output.
  
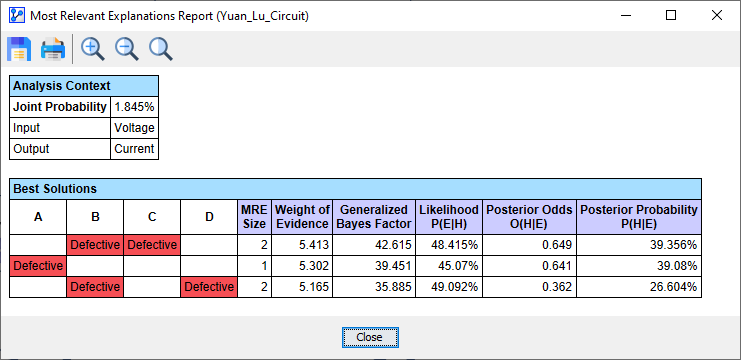
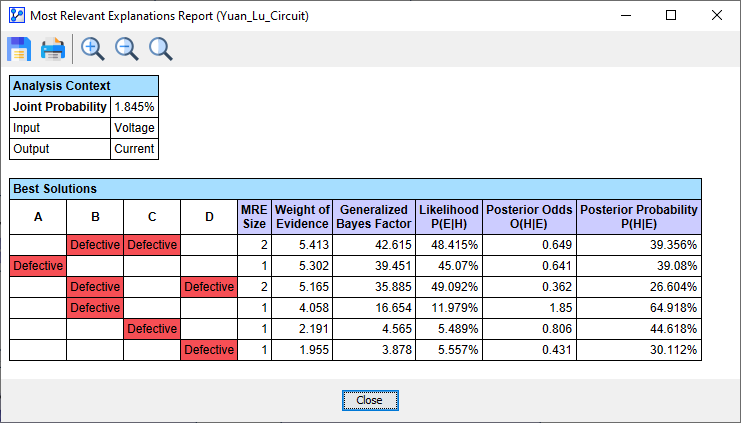
• Upon clicking OK, BayesiaLab starts the search and quickly brings up a report showing a list of solutions, i.e., explanations.
  
• In the list of Best Solutions, the top line shows the most relevant explanation H* for the observed evidence :
  • Both B and C are defective.
  • Additionally, several measures corresponding to H* are reported in the columns to the right:
    • MRE Size refers to the number of individual pieces of evidence that are part of H*, which is 2 for B and C.
    • Generalized Bayes Factor (GBF): Given that our network is a causal model, we can use the likelihood ratio to interpreting GBF. This means that the likelihood of "B=defective and C=defective" being the cause of E is 42 times greater than the likelihood of  "B=OK and C=OK" being the cause of E, i.e., 48.4% versus 1.1%.
    • Likelihood P(E|H)
    • Posterior Odds O(H|E)
    • Posterior Probability P(H|E)

Filtering Solutions

• In this example, the number of solutions is manageable. In more complex situations, however, the search algorithm could potentially find thousands of solutions.
• For constraining the size of the report, you can select the Filtering Power for producing the report.

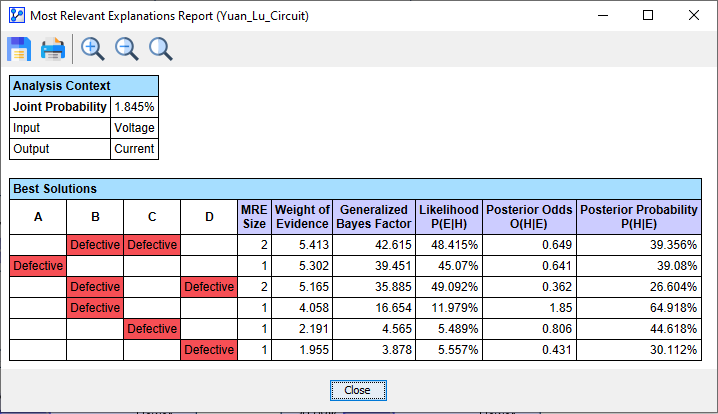
Filtering Power=0 (No Filtering)

Filtering Power=1 (Strongly Dominated Solutions are Filtered)

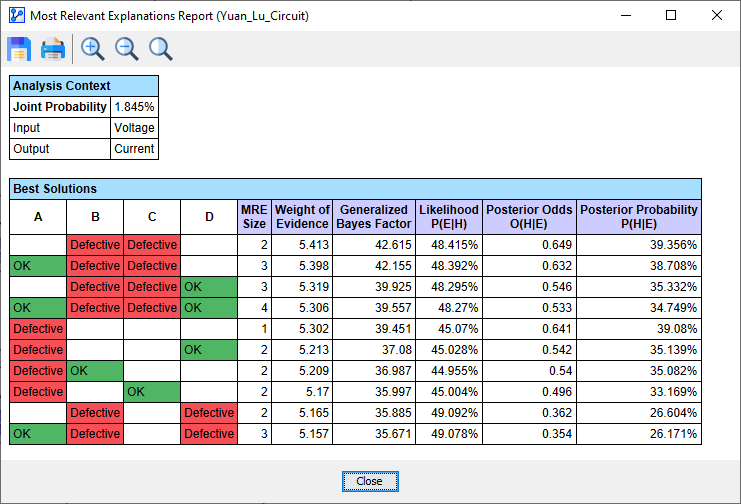
Filtering Power=2 (Strongly and Weakly Dominated Solutions are Filtered)

Workflow Animation