Means and Values of Nodes

Context
At the top of each Monitor, the items Mean, Dev, and Value are displayed.
Mean refers to the Mean Value m and is only shown in the Monitors of numerical nodes.
Dev stands for Standard Deviation and is shown alongside Mean.
Value refers to the Expected Value vvv
 and is shown in all Monitors, regardless of the node type, i.e., categorical or numerical.
Examples
The calculations for Expected Value and Mean Value are shown in the context of the following examples:
Categorical Node
Let's take the discrete node Age with three categorical Node States:
Child
Adult
Senior
Categorial Node with Assigned State Values
In the Node Editor, you can assign State Values to the Node States of Age.
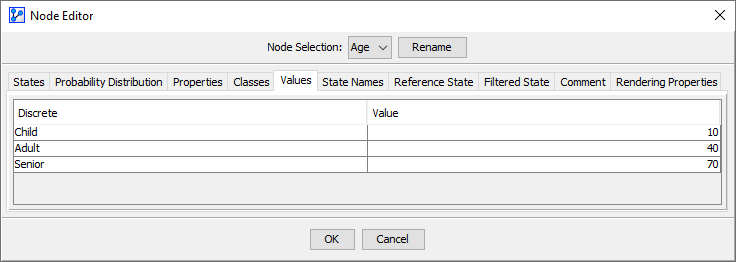
For each node, the Expected Value vvv
 is computed using the assigned State Values and the marginal probability distribution of the Node States:
​v=∑s∈Sps×Vsv = \sum_{s \in S} p_s \times V_sv=∑s∈S​ps​×Vs​
​
where ppp
 is the marginal probability of state sss
 and VsV_sVs​
 is its associated value.
​v=0.23×10+0.415×40+0.355×70=43.750v = 0.23 \times 10 + 0.415 \times 40 + 0.355 \times 70 = 43.750v=0.23×10+0.415×40+0.355×70=43.750
​
The Monitor shows vvv
 as the Value of Age.
A Monitor of a categorical node does not show a Mean value.
Discrete Numerical Variable
Let's suppose that the node Age has three numerical Node States instead of categorical Node States.

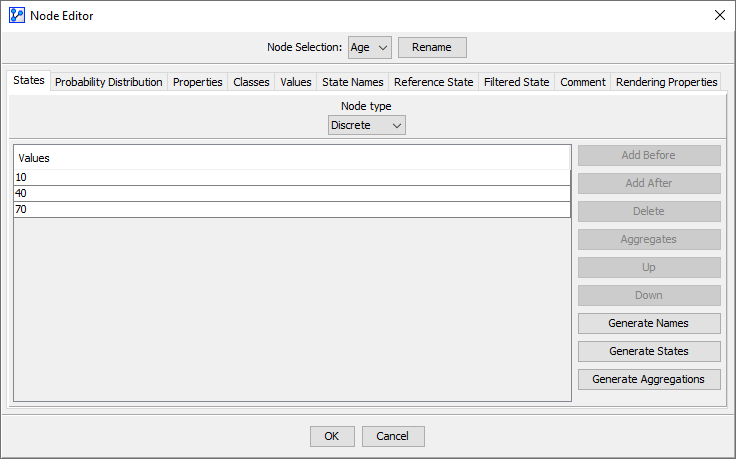
In this context, we need to consider two conditions, with and without State Values specified in the Node Editor: 
No State Values Specified
Here, State Values are not specified in the Values tab of the Node Editor. Note the empty Value column below.
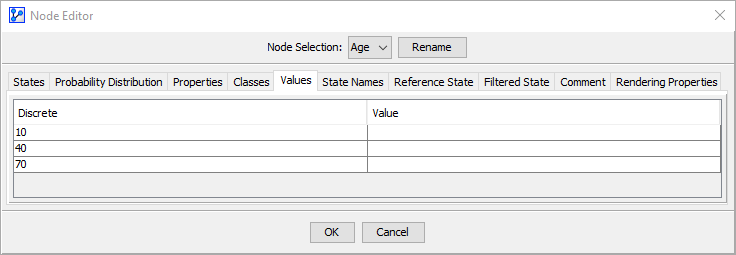
As a result, BayesiaLab uses the numerical values of the Node States, as they appear in the States tab, as the State Values.
Furthermore, as Age is a numerical node, its Monitor will now display the Mean (Mean) and the Standard Deviation (Dev) in addition to the Expected Value (Value)
The Mean m is computed using the numerical values of the Node States and the marginal probability distribution of the Node States:
​m=∑s∈Sps×csm = \sum_{s \in S} p_s \times c_sm=∑s∈S​ps​×cs​
​
where csc_scs​
 is the numerical value of the Node State.
​m=0.23×10+0.415×40+0.355×70=43.750m = 0.23 \times 10 + 0.415 \times 40 + 0.355 \times 70 = 43.750m=0.23×10+0.415×40+0.355×70=43.750
​
Note that Mean and Value are identical in this case.
State Values Specified
However, if State Values are separately specified in the Values tab of the Node Editor, they will be used for the calculation of Value in the Monitor.
To highlight the distinction between the Node States {10, 40, 70} and the State Values, we assign unrelated arbitrary State Values of 0, 1, and 2.
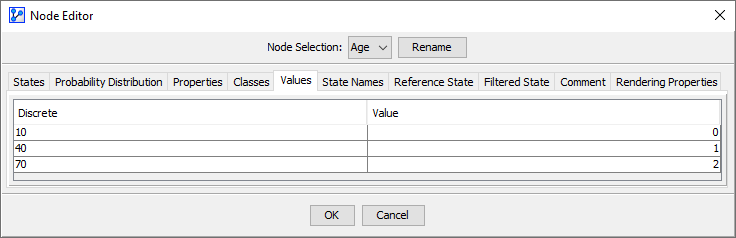
The Expected Value vvv
 is computed now using the assigned State Values {0, 1, 2} and the marginal probability distribution of the Node States:
​v=∑s∈Sps×Vsv = \sum_{s \in S} p_s \times V_sv=∑s∈S​ps​×Vs​
​
where ppp
 is the marginal probability of state sss
 and VsV_sVs​
 is its associated value.
​v=0.23×0+0.415×1+0.355×2=1.125v = 0.23 \times 0 + 0.415 \times 1 + 0.355 \times 2 = 1.125v=0.23×0+0.415×1+0.355×2=1.125
​
The Monitor shows vvv
 as the Value of Age.
Note that Mean and Value are not identical in this case.
Continuous Numerical Variable
Let's now consider a continuous variable Age defined in the domain [0; 99], discretized into three states:
Child: [0 ; 18]
Adult: ]18 ; 65]
Senior: ]65 ; 99]
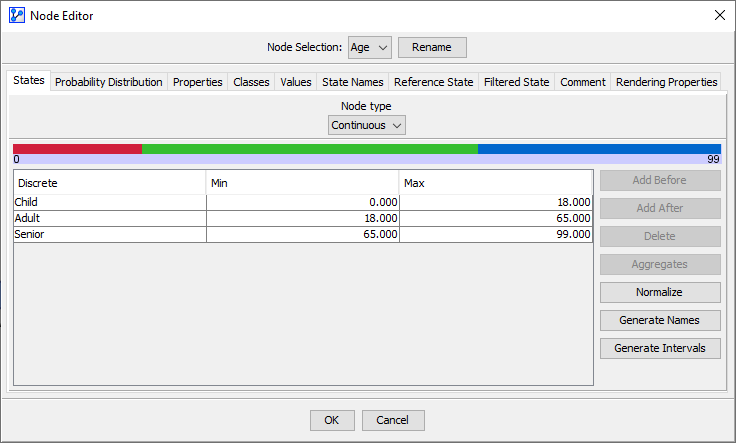
Given Age is a numerical node, its Monitor shows the Mean (Mean), the Standard Deviation (Dev), plus the Expected Value (Value).
No Associated Data
If no associated data is with the node, both csc_scs​
 and VsV_sVs​
 are defined as the mid-points of the minimum and maximum values of each Node State. For example, for the Node State Adult ]18; 65], the midpoint is 17.2225.
So, the Mean Value m is computed as follows:
​m=∑s∈Sps×csm = \sum_{s \in S} p_s \times c_sm=∑s∈S​ps​×cs​
​
​m=0.23×9+0.415×41.5+0.355×82=48.4025m = 0.23 \times 9 + 0.415 \times 41.5 + 0.355 \times 82 = 48.4025m=0.23×9+0.415×41.5+0.355×82=48.4025
​
The Expected Value vvv
 is calculated analogously:
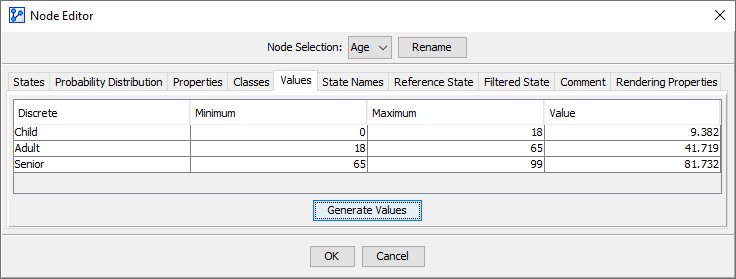
​v=∑s∈Sps×Vsv = \sum_{s \in S} p_s \times V_sv=∑s∈S​ps​×Vs​
​
​v=0.23×9+0.415×41.5+0.355×82=48.4025v = 0.23 \times 9 + 0.415 \times 41.5 + 0.355 \times 82 = 48.4025v=0.23×9+0.415×41.5+0.355×82=48.4025


Associated Data
If data is associated with the node, csc_scs​
 is defined as the arithmetic mean of the data points that are associated with each Node State.
Furthermore, clicking on the Generate Values button in the Node Editor sets the values VsVsVs
 to the current arithmetic means of each Node State.
Value Delta
If you set a new piece of evidence on a node that modifies the distribution of the node, the Monitor displays a delta value in parentheses adjacent to Value.
​
​
This delta is the difference between the current Expected Valuev and:
the Expected Value vvv
 before setting the modifying evidence, or
the Expected Value vvv
 that corresponds to the Reference Probability Distribution, which you can set with the 
 icon in the toolbar.
Special Case: Some Node States Without Values
If only some Node States have an associated value, the Expected Value vvv
 is computed from the subset of Node States S∗{S^*}S∗
 that do have an associated value.
​v=∑s∈S∗psP∗×Vsv = \sum_{s \in S^*} \frac{p_s}{P^*} \times V_sv=∑s∈S∗​P∗ps​​×Vs​
​
If a node only has a single Node State with an associated value, the corresponding Monitor does not report the Expected Value vvv
.
Latent Variables, Factors, and Hidden Nodes vs. Manifest Variables
Mutual Information
Last modified 1mo ago